- 数列
- 共2062题
16.某校数学课外小组在坐标纸上,为学校的一块空地设计植树方案如下:第








正确答案
(2,403)
解析
根据题意,




将上述k个式子相加得,
同理由



将上述k个式子相加得,
∴第2012棵树种植点的坐标为(2,403).
故答案为(2,403).
知识点
12.数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.在数列

(1)求数列
(2)若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知数列




(Ⅰ)求
(Ⅱ)求数列
正确答案
(Ⅰ)当





∴c=2.∵a2=4,即
∴

综上所述
(Ⅱ)
则
(1)

解析
解析已在路上飞奔,马上就到!
知识点
16.设
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.数列{an}中,a1=8,a4=2且满足an+2=2an+1-an,(n∈N*)。
(1)求数列{an}的通项公式;
(2)设Sn=|a1|+|a2|+…+|an|,求Sn。
正确答案
解:(1)由an+2=2an+1-an
d=
(2)由an=10-2n≥0可得n≤5,当n≤5时,Sn=-n2+9n,当n>5时,Sn=n2-9n+40,故Sn=
解析
解析已在路上飞奔,马上就到!
知识点
19.已知:对于数列


(1)若数列



(2)若数列

①设


②求:数列


正确答案
解:(1)依题意
(2)①由
∵


故



∵
∴

⑴-⑵得 
∴
解析
解析已在路上飞奔,马上就到!
知识点
22.若






(1)求数列
(2)设数列




(3)设集合







正确答案
(1)∵


作差得:
又
所以
(2)
(3)对任意

∵

∴
设等差数列

∵
而

∴
∴
解析
解析已在路上飞奔,马上就到!
知识点
11.已知数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知数列






(Ⅰ)求数列

(Ⅱ)设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.在正整数数列中,由1开始依次按如下规则将某些数染成红色.先染1,再染2个偶数2、4;再染4后面最邻近的3个连续奇数5、7、9;再染9后面最邻近的4个连续偶数10、12、14、16;再染16后面最邻近的5个连续奇数17、19、21、23、25.按此规则一直染下去,得到一红色子数列1,2,4,5,7,9,10,12,14,16,17,….则在这个红色子数列中,由1开始的第60个数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.数列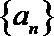
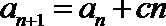


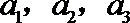

(I)求
(II)求
正确答案
答案:(I)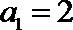
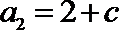

因为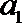
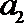
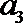
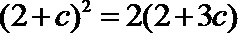
解得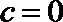
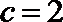
当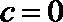
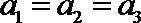
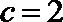
(II)当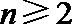
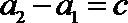

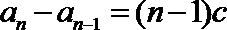
所以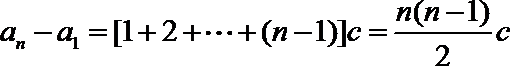
又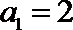
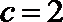
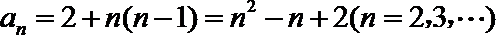
当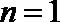
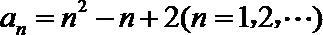
解析
解析已在路上飞奔,马上就到!
知识点
20. 设数列{an}的前n项和为Sn,对任意的正整数n,都有an =5Sn+1成立,记
(I)求数列{an}与数列{bn}的通项公式;
(Ⅱ)设数列{ bn }的前n项和为Rn,是否存存正整数k,使得Rn≥4k成立?若存在,找出一个正整数k;若不存在,请说明理由;
(III)记


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.已知正项数列
(I)求

(II)若
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析