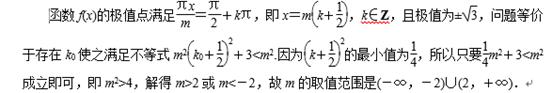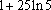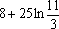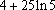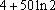- 正弦函数的定义域和值域
- 共124题
1
题型:填空题
|
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
1
题型:填空题
|
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
1
题型:填空题
|
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
1
题型:
单选题
|
设函数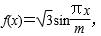
正确答案
C
解析
知识点
函数零点的判断和求解正弦函数的定义域和值域
1
题型:简答题
|
已知函数
(1) 当m=0时,求

(2) 当

正确答案
(1)
(2)m=-2
解析
(1)当m=0时,


从而得:
(2)
化简得:
当


代入上式,m=-2.
知识点
正弦函数的定义域和值域三角函数中的恒等变换应用运用诱导公式化简求值
1
题型:
单选题
|
一辆汽车在高速公路上行驶,由于遇到紧急情况而刹车,以速度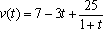
正确答案
C
解析
略
知识点
正弦函数的定义域和值域
1
题型:
单选题
|
函数
正确答案
B
解析
f(x)=sinx-cos(x+





知识点
正弦函数的定义域和值域三角函数中的恒等变换应用
1
题型:简答题
|
已知函

(1)求函数
(2)若函数

面积.
正确答案
见解析。
解析
(1)解:∵


∵



∴
(2)解法1:∵

∴
∴
∴
∴
∴△

解法2:∵

∴
∴
∴
∴
∴△

解法3:∵

∴
∴直线


∴点


∵
∴△

知识点
正弦函数的定义域和值域
1
题型:
单选题
|
由曲线


正确答案
C
解析
用定积分求解
知识点
正弦函数的定义域和值域
1
题型:填空题
|
若函数

正确答案
0
解析
∵

即

知识点
正弦函数的定义域和值域
下一知识点 : 正弦函数的单调性
扫码查看完整答案与解析