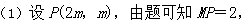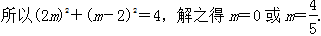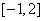- 正弦函数的定义域和值域
- 共124题
已知函数
(1)若函数f(x)的图象在
(2)求函数f(x)的单调区间;
(3)若函数
正确答案
见解析。
解析
(1)
由已知

(2)函数

①当



②当

当

由上表可知,函数

单调递增区间是
(3)由

由已知函数

则

即

即

令


所以


所以
知识点
已知数列



(1)求数列
(2)记数列




正确答案
见解析。
解析
(1)由

∴数列

∴
∴



累加得
∴

(2)由(1)利用分组求和法得




∴使得

知识点
已知椭圆

(1)求椭圆C的方程;
(2)设过点M且斜率不为0的直线交椭圆C于A,B两点,试问x轴上是否存在定点P,使PM平分∠APB?若存在,求出点P的坐标;若不存在,说明理由,
正确答案
见解析。
解析
(1)由 

因为

所以

所以椭圆

(2)设



将直线

消去

所以 

若



所以
设

将 

整理得 
所以 
将 

整理得 
由于上式对任意实数

综上,存在定点


知识点
17.已知a=(sinx,-cosx),

(1)求f(x)的最小正周期;
(2)当
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数

(Ⅰ)求F(x)的单调区间;
(Ⅱ)若以



(Ⅲ)是否存在实数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知圆M的方程为x2+(y-2)2=1,直线l的方程为x-2y=0,点P在直线l上,过点P作圆M的切线PA,PB,切点为A,B。
(1)若∠APB=60°,试求点P的坐标;
(2)若P点的坐标为(2,1),过P作直线与圆M交于C,D两点,当CD=时,求直线CD的方程;
(3)求证:经过A,P,M三点的圆必过定点,并求出所有定点的坐标。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.在△ABC中,若sin2A+sin2B-sin Asin B=sin2C,且满足ab=4,则该三角形的面积为_______。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知:函数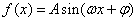
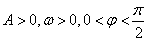

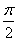
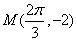
(1)求:
(2)当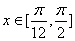
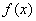
正确答案
(1)由最低点为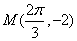

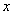
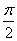
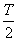
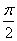
即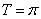
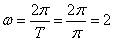
由点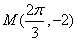
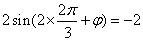
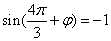
∵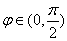
∴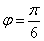
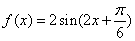
(2)∵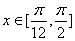
∴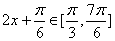
当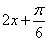
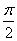
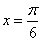

当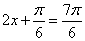
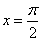
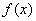
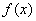
解析
解析已在路上飞奔,马上就到!
知识点
19.已知过点A(0,4)的直线l与以F为焦点的抛物线C:x2=py相切于点T(-4,yo);中心在坐标原点,一个焦点为F的椭圆与直线l有公共点.
(1)求直线l的方程和焦点F的坐标;
(2)求当椭圆的离心率最大时椭圆的方程;
(3)设点M(x1,yl)是抛物线C上任意一点,D(0,-2)为定点,是否存在垂直于y轴的直线l/被以MD为直径的圆截得的弦长为定值?请说明理由.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.△ABC中,内角A、B、C所对边分别为a、b、c,已知A=
(1)求a的长及B的大小;
(2)若0<x≤B,求函数f(x)=2sinxcosx+2cos2x-的值域。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析