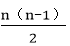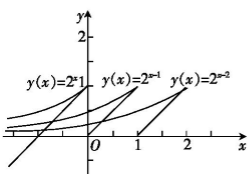- 函数与方程
- 共222题
9.已知函数y = f (x) 和 y = g (x) 的定义域及值域均为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.若函数f(x)=|2x-1|,则函数g(x)=f(f(x))+ln x在(0,1)上不同的零点个数为 .
正确答案
3
解析
将函数g(x)=f(f(x))+ln x在(0,1)上不同的零点个数转化为函数y=f[f(x)]的图象在(0,1)上与y=-ln x的图象的交点个数,
作出图象如图,可知两个函数图象在(0,1)上有3个交点,
即不同的零点个数为3.
知识点
6.已知函数f(x)=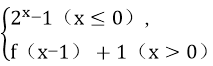
正确答案
解析
当x∈(-∞,0]时,由g(x)=f(x)-x=2x-1-x=0,得2x=x+1.令y=2x,y=x+1.在同一个坐标系内作出两函数在区间(-∞,0]上的图象,如图,
由图象易知交点为(0,1),故得到函数的零点为x=0.
当x∈(0,1]时,x-1∈(-1,0],f(x)=f(x-1)+1=2x-1-1+1=2x-1,由g(x)=f(x)-x=2x-1-x=0,得2x-1=x.令y=2x-1,y=x.在同一个坐标系内作出两函数在区间(0,1]上的图象,由图象易知交点为(1,1),故得到函数的零点为x=1.
当x∈(1,2]时,x-1∈(0,1],f(x)=f(x-1)+1=2x-1-1+1=2x-2+1,由g(x)=f(x)-x=2x-2+1-x=0,得2x-2=x-1.令y=2x-2,y=x-1.在同一个坐标系内作出两函数在区间(1,2]上的图象,由图象易知交点为(2,1),故得到函数的零点为x=2.
依此类推,当x∈(2,3],x∈(3,4],…,x∈(n,n+1]时,构造的两函数图象的交点依次为(3,1),(4,1),…,(n+1,1),得对应的零点分别为x=3,x=4,…,x=n+1.
故所有的零点从小到大依次排列为0,1,2,…,n+1.其对应的数列的通项公式为an=n-1.
知识点
12.已知定义在







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
31.定义符号函数
(1)求


(2)当



(3)已知存在



正确答案



解析
试题分析:本题属于函数中较难的问题,题目的难度是逐渐由易到难,
(1)直接按照步骤来求
(2)要注意转化后的定义域.
(1)
所以

(2)当



所以由
令

由图像可得
(3)当



所以


即

从而只需求







对于函数

(i)
(ii)
(iii)
综上,
考查方向
本题考查了绝对值函数及零点的知识.
解题思路
本题考查绝对值函数,解题步骤如下:
1、利用定义表示函数求解。
2、利用函数图像求解。
3、利用分类讨论求解。
易错点
利用定义表示函数时容易出错。
知识点
13.已知函数

取值范围是___________
正确答案
解析
∵



∴





当直线与

当

当

当









考查方向
解题思路
本题考查运用导数解决函数的能力,解题步骤如下: 先求导,找函数的切线方程,再利用零点的判定方法,找到a的取值范围。
易错点
本题必须注意审题,忽视则会出现错误。
知识点
6.若函数

正确答案
解析
∵
∴方程

∴函数

由图可知
∴
考查方向
本题主要考查函数的性质,考查数形结合、函数与方程的思想,是中档题,在近几年各省市的高考中出现频率很高,常将函数的几个性质结合在一起进行命题.
解题思路
作出函数


易错点
对函数零点概念的不理解,或者不能将函数零点个数转化为两个函数图像四个交点来求解.
知识点
10.设函数f(x)=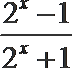
正确答案
解析
本题属于函数中的零点问题,题目的难度较大。注意对函数f(x)的值域的分析.
考查方向
本题主要考查了函数的零点问题,在近几年的各省高考题出现的频率较高,常与基本初等函数图像、不等式含参问题等知识点交汇命题。
解题思路
无
易错点
本题易在含参的讨论上发生错误。
知识点
12.已知


正确答案
17
解析
本题主要考查了函数的图像求交点。
考查方向
本题主要考查了函数的图像求交点。
解题思路
本题考查函数图像求交点,分别作出f(x),g(x)的图像求解。
易错点
本题要注意利用图像求解。
知识点
20.已知

(1)讨论函数
(2)若函数

①求实数
②求证:
正确答案
见解析
解析
(1)


①当


②当




所以


(2)①由(I)知,当


当







所以

此时,

令

所以


所以
②证法一:
下面证明:当

设





即当






②证法二:
令
则:
所以函数



于是
又

考查方向
解题思路
1利用导数求函数单调性,2根据函数的零点求参数的取值范围
3构造函数求两个零点和的范围
易错点
本题必须注意函数的定义域,以及对参数进行讨论,否则求解错误。
知识点
扫码查看完整答案与解析