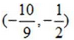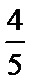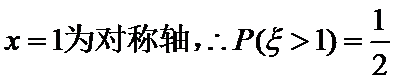- 函数与方程
- 共222题
8.已知函数f(x)=

正确答案
解析
由










考查方向
解题思路
根据函数的单调性先求出



易错点
忽略
教师点评
函数性质综合应用
知识点
14.若函数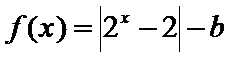
正确答案
(-2,+∞)
考查方向
易错点
1.不注意指数函数的有界性导致出错;
知识点
14.设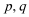
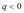
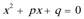
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知开口向上的二次函数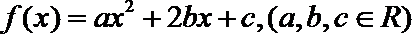
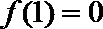
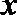
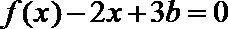
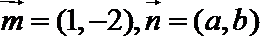
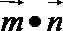

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知二次函数



(1)求
(2)若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若函数f(x)=x2-ax+2在区间[0,1]上至少有一个零点,则实数a的取值范围是__________.
正确答案
[3,+∞)
解析
由题意,
知关于x的方程x2-ax+2=0在区间[0,1]上有实数解.
又x=0不是方程x2-ax+2=0的解,
所以根据0<x≤1
可将方程x2-ax+2=0变形为
从而问题转化为求函数
因为函数g(x)在(0,1]上单调递减,
所以g(x)∈[3,+∞).
故所求实数a的取值范围是[3,+∞)。
知识点
10.若方程x2-4|x|+5-m=0恰有4个不同的实数解,则实数m的取值范围是 .
正确答案
(1,5)
解析
设函数
函数y2=m,则方程x2-4|x|+5=m的实数解就是函数y1与y2图象交点的横坐标,
当方程x2-4|x|+5=m有4个不同的实数解时,
两个函数的图象应有4个不同的交点,
在同一直角坐标系中作出两个函数的图象,
如图所示,
则可得实数m的取值范围是(1,5).
知识点
2.函数f(x)=x2-
正确答案
解析
显然
若函数在区间(1,2)上有零点,则
解得-1<a<3.
所以当函数
实数a的取值范围为(-∞,-1]∪[3,+∞).
知识点
12.已知函数



正确答案
解析





又因为




考查方向
解题思路
利用正弦曲线的对称性,知道





易错点
不会作出分段函数图像,找不到对称关系。
知识点
3.设随机变量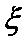
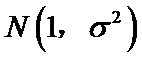
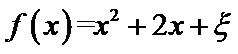
正确答案
解析
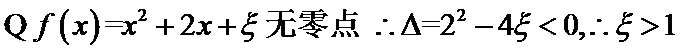
考查方向
解题思路
【解题思路】本题属于简单题,可使用直接法,
易错点
该题容易忽视正态分布曲线的对称性
知识点
扫码查看完整答案与解析