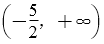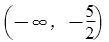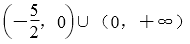- 平面向量的数量积及其应用
- 共703题
10.定义:平面内两条相交但不垂直的数轴构成的坐标系(两条数轴的原点重合且单位长度相同)称为平面的斜坐标系;在平面的斜坐标系














正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知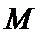
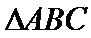
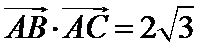
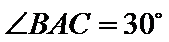
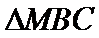
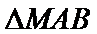
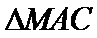
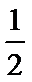
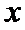
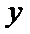
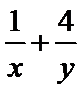
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 已知非零向量





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知向量
(1)求
(2)设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 在平面直角坐标系

(1)求向量

(2)若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知a=(1,3),b=(1,1),c=a+λb,若a和c的夹角是锐角,则λ的取值范围是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.若|a|=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知点P(4,4),圆C:

(1)求m的值与椭圆E的方程;
(2)设Q为椭圆E上的一个动点,求
正确答案
(1)点A代入圆C方程,得
圆C:

即


当k=

当k=

2a=|AF1|+|AF2|=

椭圆E的方程为:
(2)


∵


所以,


解析
解析已在路上飞奔,马上就到!
知识点
10.如图所示,等边△ABC的边长为2,D为AC中点,且△ADE也是等边三角形,在△ADE以点A为中心向下转动到稳定位置的过程中,
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数


(1)求函数
(2)在△






正确答案
(1)
由

∴
(2)由



∴



再由余弦定理得,
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析