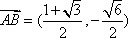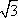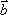- 平面向量的数量积及其应用
- 共703题
5.设


①若

②若

③若


④若

其中真命
正确答案
解析
第1个,两直线也可能为异面直线,故错误,第2个正确,第三个也可能是m在平面呢,故错误,第4个比如正方体的相邻的三个面,就是反例,所以真命题只有1个,所以选B
考查方向
解题思路
根据直线与平面的位置关系的特征,逐一判断
易错点
考虑直线和平面位置关系考虑不周全
知识点
6.若非零向量a,b满足|a|=

正确答案
解析
由题意




考查方向
解题思路
本题考查两向量的夹角,涉及到向量的模,向量的垂直,向量的数量积等知识,体现了数学问题的综合性,考查学生运算求解能力,综合运用能力.
易错点
向量数量积运算的化简
知识点
8.已知向量












正确答案
解析
根据题意可知,
由
可得
所以
考查方向
向量的线性运算与向量的数量积
解题思路
根据题意先表示出向量夹角的坐标形式,然后求解
易错点
对向量的数量积性质掌握不牢
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
某算法的程序框图如图所示,其中输入的变量x在1,2,3,…,24这24个整数中等可能随机产生。
(1)分别求出按程序框图正确编程运行时输出y的值为i的概率Pi(i=1,2,3);
(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录了输出y的值为i(i=1,2,3)的频数,以下是甲、乙所作频数统计表的部分数据。
当n=2 100时,根据表中的数据,分别写出甲、乙所编程序各自输出y的值为i(i=1,2,3)的频率(用分数表示),并判断两位同学中哪一位所编程序符合算法要求的可能性较大;
(3)将按程序框图正确编写的程序运行3次,求输出y的值为2的次数ξ的分布列及数学期望。
正确答案
见解析
解析
(1)变量x是在1,2,3,…,24这24个整数中随机产生的一个数,共有24种可能。
当x从1,3,5,7,9,11,13,15,17,19,21,23这12个数中产生时,输出y的值为1,故P1=
当x从2,4,8,10,14,16,20,22这8个数中产生时,输出y的值为2,故P2=
当x从6,12,18,24这4个数中产生时,输出y的值为3,故P3=
所以,输出y的值为1的概率为


(2)当n=2 100时,甲、乙所编程序各自输出y的值为i(i=1,2,3)的频率如下:
比较频率趋势与概率,可得乙同学所编程序符合算法要求的可能性较大。
(3)随机变量ξ可能的取值为0,1,2,3.
P(ξ=0)=
P(ξ=1)=
P(ξ=2)=
P(ξ=3)=
故ξ的分布列为
所以,Eξ=0×



即ξ的数学期望为1.
知识点
在平面直角坐标系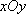
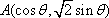
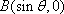
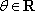
(1)当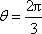
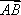
(2)当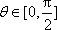
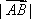
正确答案
(1)
(2)最大值
解析
(1)解:由题意,得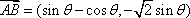
当 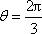
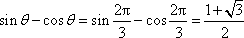
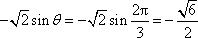
所以 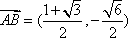
(2)解:因为 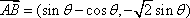
所以 
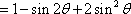
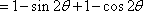
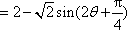
因为 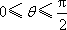
所以 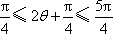
所以当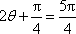
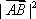
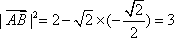
即当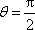
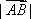
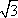
知识点
已知向量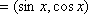
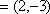
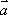

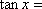
正确答案

解析
略
知识点
已知向量




正确答案
解析
略
知识点
(1)化简[(a-32b2)-1(ab-3)12(b12)7]13.
(2)解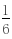
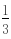
(3)用二项式定理计算(3.02)4,使误差小于千分之一.
(4)试证直角三角形弦上的半圆的面积,等于勾上半圆的面积与股上半圆的面积的总和.
(5)已知球的半径等于r,试求内接正方形的体积.
(6)已知a是三角形的一边,β及γ是这边的两邻角,试求另一边b的计算公式.
评卷人
得 分
正确答案
的发生的
知识点
扫码查看完整答案与解析