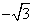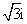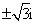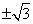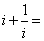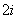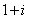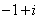数系的扩充和复数的引入
共917题

数系的扩充和复数的引入
共917题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

2，已知复数的实部为，且，则复数的虚部是

正确答案

解析

略

知识点

虚数单位i及其性质

题型：填空题

填空题 · 4 分

已知为虚数单位，计算：___________。

正确答案

解析

略

知识点

虚数单位i及其性质

题型：填空题

填空题 · 4 分

展开式中含项的系数是_________。

正确答案

解析

略

知识点

虚数单位i及其性质

题型：填空题

填空题 · 5 分

若，其中是虚数单位，则实数的值是____________.

正确答案

解析

略

知识点

虚数单位i及其性质

题型：单选题

单选题 · 5 分

已知复数 (为虚数单位），则复数在复平面上所对应的点位于（）

A第一象限

B第二象限

C第三象限

D第四象限

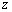
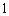
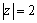
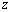
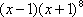
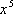
正确答案

解析

∵z=i（1+i）=﹣1+i，

∴z=i（1+i）=﹣1+i对应的点的坐标是（﹣1，1）

∴复数在复平面对应的点在第二象限。

故选B。

知识点

虚数单位i及其性质

题型：填空题

填空题 · 5 分

是虚数单位，则。

正确答案

-8i

解析

知识点

虚数单位i及其性质

题型：简答题

简答题 · 14 分

已知函数.

（1）求的单调区间；

（2）若，求证：函数只有一个零点，且；

（3）当时，记函数的零点为，若对任意且都有成立，求实数的最大值。

（本题可参考数据：）

正确答案

见解析

解析

（1）解：的定义域为.

.…………………1分

令，或.

当时，，函数与随的变化情况如下表：

所以，函数的单调递增区间是，单调递减区间是和.…………………3分

当时，. 所以，函数的单调递减区间是(-1,+ )。……………………4分

当时，，函数与随的变化情况如下表：

所以，函数的单调递增区间是，单调递减区间是和（0，+）.

…………………………5分

（2）证明：当时，由（1）知，的极小值为，极大值为.

因为，，且在上是减函数，

所以至多有一个零点.…………………7分

又因为，

所以函数只有一个零点，且.

……………………9分

（3）解：因为，

所以对任意且由(Ⅱ)可知：，，且.…………………10分

因为函数在上是增函数，在上是减函数，

所以，.…………………11分

所以.

当时，=>0.

所以…………………13分

所以的最小值为.

所以使得恒成立的的最大值为.………………14分

知识点

虚数单位i及其性质

题型：填空题

填空题 · 5 分

展开式中的常数项为　　。

正确答案

-372

解析

展开式中的常数项为Tr+1==2r×（﹣1）r

9﹣3r=0可得r=3

此时常数项为×（﹣1）=﹣372

故答案为：﹣372

知识点

虚数单位i及其性质

题型：填空题

填空题 · 5 分

复数在复平面内所对应的点在虚轴上，那么实数=（） .

正确答案

解析

略

知识点

虚数单位i及其性质

题型：填空题

填空题 · 4 分

若复数为纯虚数，则实数的值为。

正确答案

解析

略

知识点

函数的概念及其构成要素虚数单位i及其性质复数相等的充要条件

题型：单选题

单选题 · 5 分

设z=1﹣i（是虚数单位），则=（　　）

B2+i

C2﹣i

D2+2i

正确答案

解析

∵z=1﹣i，∴，==。

∴==1+i+1+i=2+2i。

故选D。

知识点

虚数单位i及其性质

题型：单选题

单选题 · 5 分

若，则a0=（　　）

B32

C-1

D-32

正确答案

解析

∵（x+1）5=[2+（x﹣1）]5=•25+•24（x﹣1）+•23•（x﹣1）2+•22（x﹣1）3+•2•（X﹣1）4+•（x﹣1）5，

而且，

故 a0=•25=32，

故选B。

知识点

虚数单位i及其性质

题型：单选题

单选题 · 5 分

在的展开式中，含的系数是

A10

B15

C20

D25

正确答案

解析

略

知识点

虚数单位i及其性质

题型：单选题

单选题 · 5 分

复数（i为虚数单位）的共轭复数是（　　）

A1-i

B1+i

正确答案

解析

因为复数==。

所以=。

故选D。

知识点

虚数单位i及其性质

题型：单选题

单选题 · 5 分

为虚数单位，则

正确答案

解析

略

知识点

虚数单位i及其性质

继续学习学习下一知识点

下一知识点 : 推理与证明

百度题库 > 高考 > 理科数学 > 数系的扩充和复数的引入

扫码查看完整答案与解析