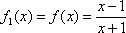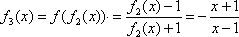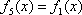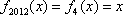- 推理与证明
- 共88题
设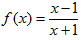
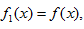
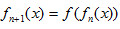
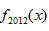
正确答案
x
解析
由题目可预知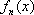
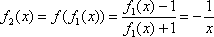
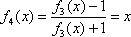
……,可知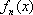
知识点
观察下列不等式:
①


正确答案
解析
解:由①
②
③
归纳可知第四个不等式应为
第五个不等式应为
故答案为
知识点
某商场调查旅游鞋的销售情况,随机抽取了部分顾客的购鞋尺寸,整理得如下频率分布直方图,其中直方图从左至右的前3个小矩形的面积之比为

正确答案
55%
解析
后两个小组的频率为






知识点
某辆汽车购买时的费用是15万元,每年使用的保险费、路桥费、汽油费等约为1.5万 元,年维修保养费用第一年3000元,以后逐年递增3000元,则这辆汽车报废的最佳年 限(即使用多少年的年平均费用最少)是( )
正确答案
解析
设这辆汽车报废的最佳年限n年,第n年的费用为an,则
an=1.5+0.3n,
前n年的总费用为:
Sn=15+1.5n+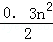
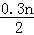
年平均费用: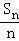
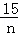
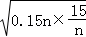
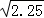
当且仅当0.15n=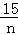
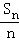
所以则这辆汽车报废的最佳年限10年。
故选B。
知识点
观察下列各式:a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…,则a10+b10=( )
正确答案
解析
利用归纳法:a+b=1,a2+b2=3,a3+b3=4=3+1,a4+b4=4+3=7,a5+b5=7+4=11,a6+b6=11+7=18,a7+b7=18+11=29,a8+b8=29+18=47,a9+b9=47+29=76,a10+b10=76+47=123.
规律为从第三组开始,其结果为前两组结果的和。
知识点
已知



正确答案
解析
如图所示,
∴




知识点
8.对于定义域和值域均为[0,1]的函数f(x),定义






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.如图所示,将数以斜线作如下分群:(1),(2,3),(4,6,5),(8,12,10,7),(16,24,20,14,9),…,并顺次称其为第1群,第2群,第3群,第4群,…,
(1)第7群中的第2项是( );
(2)第n群中n个数的和是( ).
正确答案
(1)96
(2)3·2n-2n-3
解析
解析已在路上飞奔,马上就到!
知识点
15.我们把平面内与直线垂直的非零向量称为直线的法向量,在平面直角坐标系中利用动点轨迹的方法,可以求出过点





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.设数列
(1)当


(2)当

(i)
(ii)
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.已知数集





(1)分别判断数集


(2)求


(3)由(2)及通过对

正确答案
(1)由于



由于








(2)∵




从而
当




从而



故数列
(3)命题一:对于一切大于或等于3的奇数


证明:由(2),不妨设





因为







第1组:

第2组:

第3组:

第


上一组的第2项总大于下一组的第1项,再注意到
第1组的各数从左到右依次为:
第2组的各数从左到右依次为:
第3组的各数从左到右依次为:
第

于是,有
由(﹡),




成等比数列.
命题二:对于一切大于或等于6的偶数


证略(同命题一的证明类似)
命题三:对于一切





(证略)若学生指出:当


例如数列

解析
解析已在路上飞奔,马上就到!
知识点
15.
正确答案
-7
解析
解析已在路上飞奔,马上就到!
知识点
15.由下面四个图形中的点数分别给出了四个数列的前四项,将每个图形的层数增加可得到这四个数列的后继项,按图中多边形的边数依次称这些数列为“三角形数列”、“四边形数列”…,将构图边数增加到n可得到“n边形数列”,记它的第r项为P(n,r),则
(1)使得P(3,r)>36的最小r的取值是____;
(2)试推导P(n,r)关于,n、r的解析式是____.
正确答案
(1)
(2)

解析
解析已在路上飞奔,马上就到!
知识点
8.如图一个倒三角形数表:它的排列规则是:第






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 把正整数排列成如图甲的三角形数阵,然后擦去第偶数行的奇数和第奇数行中的偶数,得到如图乙的三角数阵,再把图乙中的数按从小到大的顺序排成一列,得到数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析