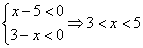- 数系的扩充和复数的引入
- 共917题
若复数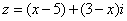
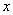
正确答案
解析
由题意可知,
知识点
某中学举行了一次田径运动会,其中有50名学生参加了一次百米比赛,他们的成绩和频率如图所示.若将成绩小于15秒作为奖励的条件,则在这次百米比赛中获奖的人数共有 ▲ 人.
正确答案
11
解析
由图知,成绩在

所以这次百米比赛中获奖的人数共有11人
知识点
已知复数


正确答案
解析
略
知识点
若

正确答案
解析
略
知识点
在
正确答案
45
解析



知识点
设i为虚数单位,则复数
正确答案
解析
知识点
设复数z满足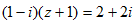
正确答案
解析
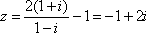
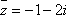
知识点
已知

(1)求
(2)若


正确答案
见解析
解析
解析:(1)设


由
得
解得

∴

(2)当


当

∴
知识点
已知复数

正确答案
解析
略
知识点
二项式

正确答案
-126
解析
略
知识点
设



正确答案
解析


因此

又

因此,
知识点
设g(x)=ex,f(x)=g[λx+(1﹣λ)a]﹣λg(x),其中a,λ是常数,且0<λ<1。
(1)求函数f(x)的极值;
(2)证明:对任意正数a,存在正数x,使不等式
(3)设

正确答案
见解析。
解析
解:(1)∵f′(x)=λg[λx+(1﹣λ)a]﹣λg′(x),)
由f′(x)>0得,g[λx+(1﹣λ)a]>g′(x),
∴λx+(1﹣λ)a>x,即(1﹣λ)(x﹣a)<0,解得x<a
故当x<a时,f′(x)>0;当x>a时,f′(x)<0;
∴当x=a时,f(x)取极大值,但f(x)没有极小值。
(2)∵
又当x>0时,令h(x)=ex﹣x﹣1,则h′(x)=ex﹣1>0,
故h(x)>h(0)=0,
因此原不等式化为
令g(x)=ex﹣(1+a)x﹣1,则g′(x)=ex﹣(1+a),
由g′(x)=0得:ex=(1+a),解得x=ln(a+1),
当0<x<ln(a+1)时,g′(x)<0;当x>ln(a+1)时,g′(x)>0。
故当x=ln(a+1)时,g(x)取最小值g[ln(a+1)]=a﹣(1+a)ln(a+1),
令s(a)=

故s(a)<s(0)=0,即g[ln(a+1)]=a﹣(1+a)ln(a+1)<0。
因此,存在正数x=ln(a+1),使原不等式成立。
(3)对任意正数a1,a2,存在实数x1,x2使a1=e

则



原不等式


⇔g(λ1x1+λ2x2)≤λ1g(x1)+λ2g(x2)
由(1)f(x)≤(1﹣λ)g(a)
故g[λa+(1﹣λ)a]≤λg(x)+(1﹣λ)g(a)
令x=x1,a=x2,λ=λ1,1﹣λ=λ2
从而g(λ1x1+λ2x2)≤λ1g(x1)+λ2g(x2)
故

知识点
已知复数



(1)若复数

(2)若虚数


正确答案
见解析
解析
(1)由条件得,
因为


(2)因为虚数

所以

把

所以
知识点
设虚数




(1) 求
(


(3) 设虚数





正确答案
见解析
解析
(1)

(或
(2)



当

当

(3)解:
① 
由




② 

当
当
知识点
已知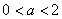
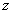
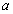
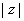
正确答案
解析
由于复数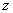
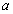
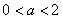
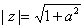
知识点
扫码查看完整答案与解析