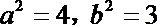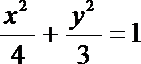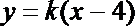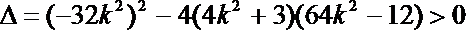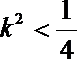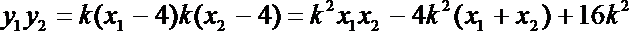- 圆锥曲线的综合问题
- 共478题
20. 如图,

(1)求证:直线CD的斜率为定值;
(2)延长DC交x轴于点E,若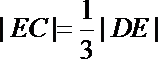

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
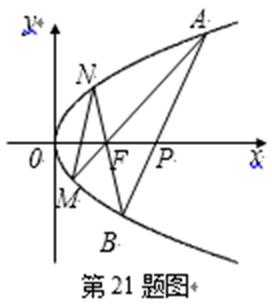
21.如图,已知抛物线






(1)证明
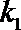


(2)记直线

正确答案
证明:(1)依题意,设直线

将其代入

整理得 
从而
于是
∴

又
(2)证明:设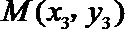
则 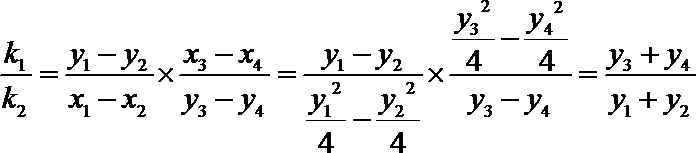
设直线

将其代入

整理得
∴
同理可得 
故
由(1)知,
∴
解析
解析已在路上飞奔,马上就到!
知识点
19.已知椭圆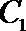
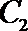

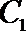

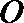
(1)求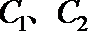
(2)过曲线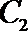
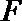
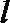
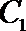
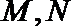
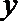
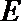
若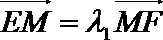
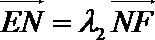
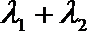
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知椭圆





(I)求椭圆方程;
(Ⅱ)若





(III)在(Ⅱ)的条件下,试问




正确答案
(I)



(Ⅱ)


直线


代入椭圆





(III)设存在


解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆C:


(Ⅰ)求椭圆C的标准方程
(Ⅱ)若直线L:
求证:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知点
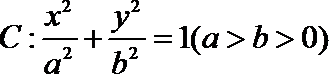
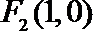
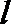
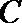
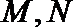
(1)求椭圆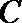
(2)若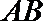
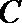
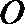
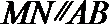
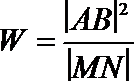
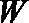
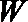
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆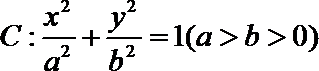

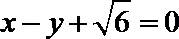
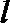
(1)求椭圆C的方程;
(2)求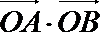
(3)若B点在于x轴的对称点是E,证明:直线AE与x轴相交于定点。
正确答案
(1)解:由题意知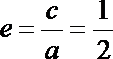
∴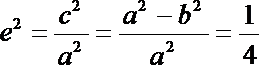
又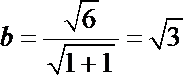
∴
故椭圆的方程为
(2)解:由题意知直线l的斜率存在,设直线l的方程为
由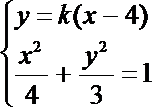
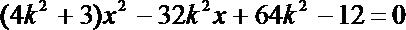
由
得:
设A(x1,y1),B (x2,y2),则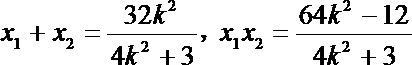
∴
解析
解析已在路上飞奔,马上就到!
知识点
21.已知椭圆C的离心率
(I)求椭圆C的方程;
(II)设直线x=my+1与椭圆C交于P,Q两点,直线A1P与A2Q交于点S,试问:当m变化时,点S是否恒在一条定直线上?若是,请写出这条直线方程,并证明你的结论;若不是,请说明理由.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆C:
(1)求椭圆C的方程;
(2)过点Q(4,0)且不与坐标轴垂直的直线l交椭圆C于A、B两点,设点A关于x轴的对称点为A1.求证:直线A1B过x轴上一定点,并求出此定点坐标.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆C:+=1(a>b>0)的离心率e=,椭圆C的上、下顶点分别为A1,A2,左、右顶点分别为B1,B2,左、右焦点分别为F1,F2.原点到直线A2B2的距离为.
(1)求椭圆C的方程;
(2)过原点且斜率为的直线l,与椭圆交于E,F点,试判断∠EF2F是锐角、直角还是钝角,并写出理由;
(3)P是椭圆上异于A1,A2的任一点,直线PA1,PA2,分别交
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析