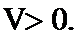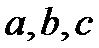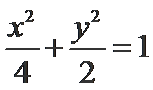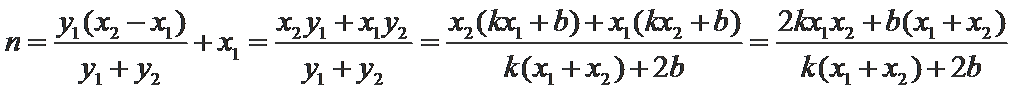- 圆锥曲线的综合问题
- 共478题
18. 已知点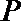
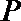
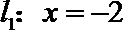
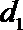
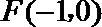
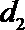
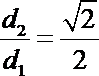
(1)求动点P所在曲线C的方程;
(2)直线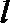
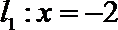
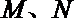
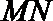
(3)记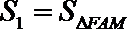
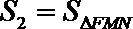
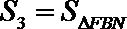
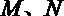
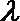
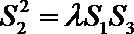
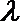
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知:向量

(1)求动点 M 的轨迹 C 的方程;
(2)已知直线







正确答案
解:设点
∵
∴
∴点 M 的轨迹C是以
∴
∴ 动点M 的轨迹 C的方程为
(2)
由(1)知,轨迹C是椭圆

设满足条件的直线



则直线

将①代入椭圆方程并整理得:


将②代入椭圆方程并整理得:

由△BDE是等腰直角三角形得
∴

∵方程④

∴即满足条件的直线

解析
解析已在路上飞奔,马上就到!
知识点
20. 已知F(







(Ⅰ)求抛物线方程和N点坐标;
(Ⅱ)判断直线




正确答案
见解析
解析
(Ⅰ)由题意

故抛物线方程为
由|NF|=

∵
∴
所以N(2,2)。
(Ⅱ)由题意知直线的斜率不为0,则可设直线

联立方程组

设两个交点A(





由

此时,
故直线


因为M(2,-2),
所以M,E所在直线平行x轴,
所以△MAB的面积



考查方向
解题思路
建立适当的坐标系,利用直线斜率之间的关系建立方程,进而求解,与抛物线联立成方程组,整理可得。
易错点
计算能力弱,找不到面积最小时候的情况
知识点
20.设椭圆



(Ⅰ)求椭圆
(Ⅱ)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆


正确答案
(Ⅰ)
(Ⅱ)
解析
试题分析:本题是直线与圆锥曲线的常见题型,运算量较大。此类问题往往要用到韦达定理,设而不求等方法技巧,把几何关系转化为代数运算。
(Ⅰ)因为




(Ⅱ)若存在满足题意的定圆,设该定圆半径为









①由上述讨论可知,切线







②当切线不与



则圆心


由

所以


所以,
所以,
所以
综上所述,存在定圆



考查方向
解题思路
本题主要考查椭圆的标准方程和几何性质,直线与椭圆的交点,直线斜率等基础知识,解题步骤如下:
(Ⅰ)把点的坐标代入,求出椭圆方程;
(Ⅱ)通过分析得出圆方程,然后对切线与X轴垂直与否,进行分类讨论,推理,得出答案。
易错点
(Ⅰ)得出定圆方程
(Ⅱ)对切线与X轴垂直与否,不能进行分类说明。
知识点
20.已知点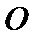
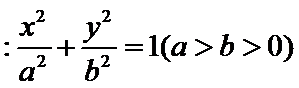
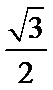
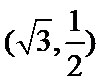
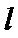
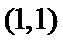
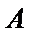
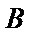
(I)求椭圆C的方程;
(Ⅱ)椭圆C上是否存在一点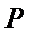
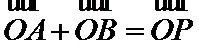
正确答案
(I)
(Ⅱ)存在直线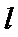
解析
(I)由题意得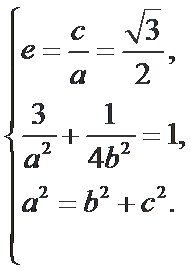
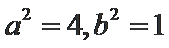
所以椭圆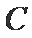
(Ⅱ)(1)当直线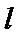
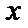
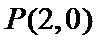
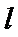
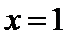
(2)当直线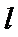
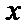
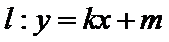
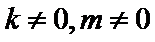
设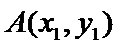
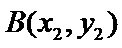
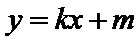
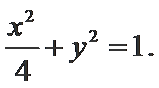
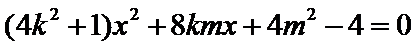
由直线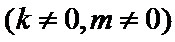
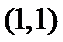
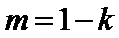
因此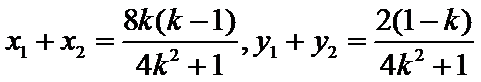
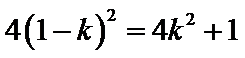
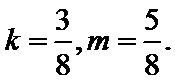
所以直线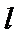
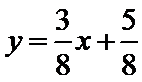
综上,椭圆C上存在点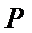
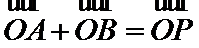
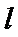
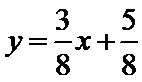
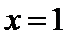
考查方向
解题思路
第一问直接根据离心率得到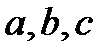
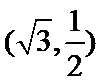
第二问设直线方程,别忘了考虑斜率不存在的情况,然后根据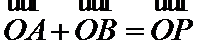
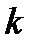
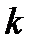
易错点
1、在第二问设斜率的时候没有考虑斜率不存在的情况;
2、在第二问中计算出错
知识点
20.已知椭






正确答案
(1)
(2)
解析
试题分析:本题属于解析几何的基本问题,题目的难度是逐渐由易到难,
(1)直接按照步骤来求
(2)要注意计算的准确性,利用三点共线解题
(1)由题意得


(2)设

由

由A,P,M三点共线可知,

所以
考查方向
本题考查了椭圆的集合性质和直线与椭圆的位置关系
解题思路
(1)由已知条件推导出
(2)设设


易错点
1、第一问中的易丢对a的分类讨论。
2、第二问计算的准确性;
知识点
19.已知椭圆C:


(Ⅰ)求椭圆C的方程;
(Ⅱ)设动直线





正确答案
(Ⅰ)
(Ⅱ)

解析
试题分析:本题属于解析几何的基本问题,题目的难度是逐渐由易到难,(1)直接按照步骤来求,(2)要注意直线不存在斜率的特殊情况,(3)要注意计算结果去正确性
(Ⅰ)解:由题意,得

又因为点

所以
解得


所以椭圆C的方程为
(Ⅱ)结论:存在符合条件的圆,且此圆的方程为
证明如下:
假设存在符合条件的圆,并设此圆的方程为
当直线


由方程组

因为直线

所以

由方程组

则
设



设直线



所以

将

要使得


所以当圆的方程为




当直线


此时,圆



综上,当圆的方程为




考查方向
本题主要考查了椭圆的标准方程、直线与椭圆的位置关系,直线与圆锥曲线的位置关系的考查主要分以下几类:
1.直线与圆锥曲线的公共点个数问题,
2.弦长问题,
3.中点弦问题.
解题思路
本题考查直线与椭圆的位置关系,解题步骤如下:
1.利用待定系数法求出椭圆的标准方程;
2.假设存在,设出圆的方程与直线方程;
3.联立直线与椭圆的方程,化简得到关于

4.联立直线与圆的方程,化简得到关于
5.讨论直线斜率不存在的情况,得到结论。
易错点
1、第二问中,联立直线与圆的方程得到关于关于
2、第二问中,不要忘记“直线无斜率”的特殊情况。
知识点
正确答案
知识点
19.




(Ⅰ)求椭圆
(Ⅱ)若点



的另一个交点为


若存在,求出点
正确答案
(Ⅰ)
(Ⅱ)不存在
解析
(Ⅰ)因为椭圆


令


又离心率为


所以
所以

(Ⅱ)法一



与椭圆方程联

化简得到
因为
所以
所以
所以
因为圆心到直线

所以
因为
代入得到
显然


法二:设点


与椭圆方程联立得
化简得到


显然
所以另一个根,
即
由
因为圆心到直线

所以
因为
代入得到
若


所以不存在直线

法三:假设存在点



显然直线


由

由

所以
同理可得
所以由

则

所以不存在直线

考查方向
本题主要考察了椭圆的方程与直线与椭圆的位置关系问题:
一是会用待定系数法求椭圆的方程;
二是会用熟悉用根与系数的关系解决直线和圆锥曲线的位置关系问题。
易错点
1、本题易在用待定系数法用错导致圆锥曲线方程算错。
2、本题用根与系数的关系时运算出错导致后面全部错误。
知识点
21.已知椭圆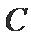
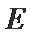
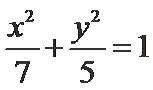
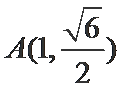
(1)求椭圆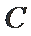
(2)在椭圆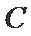
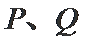
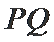
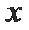
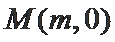
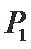
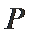
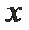
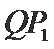
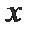
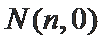
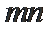
正确答案
(1)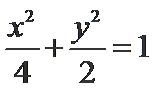
(2)定值为4.
解析
(1)
(2)当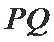
故设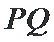
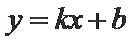
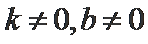
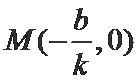
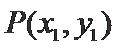
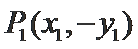
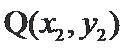
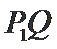
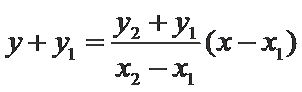
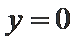
由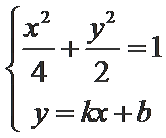
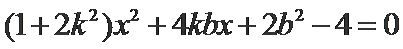
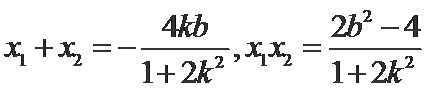
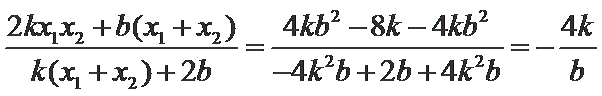
故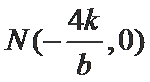
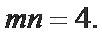
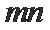
考查方向
本题主要考查直线与椭圆的位置关系和性质。
解题思路
设出直线方程,与椭圆方程联立,巧用韦达定理设而不求。
易错点
第二问中运算较烦,学生没有耐心,不细心,所以很容易出错。
知识点
扫码查看完整答案与解析