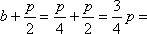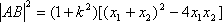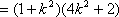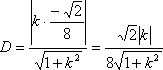- 圆锥曲线的综合问题
- 共478题
如图,设椭圆C:

(1) 已知直线


(2) 若过原点





正确答案
见解析
解析
(1)方法1:设直线l的方程为

由于直线l与椭圆C只有一个公共点P,故△=0,即
又点P在第一象限,故点P的坐标为
方法2:作变换


切点




在圆



由
即

所以

即


利用逆变换
(2)由于直线l1过原点O且与直线l垂直,故直线l1的方程为x+ky=0,所以点P到直线l1的距离

因为
当且仅当
所以,点P到直线
知识点
如图,点









(1)求椭圆
(2)求

正确答案
(1)
解析
(1)由已知得到


(2)因为直线









由


当
知识点
在平面直角坐标系xOy中,F是抛物线C:x2=2py(p>0)的焦点,M是抛物线C上位于第一象限内的任意一点,过M,F,O三点的圆的圆心为Q,点Q到抛物线C的准线的距离为
(1)求抛物线C的方程;
(2)是否存在点M,使得直线MQ与抛物线C相切于点M?若存在,求出点M的坐标;若不存在,说明理由;
(3)若点M的横坐标为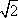


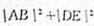
正确答案
见解析。
解析
(1)F抛物线C:x2=2py(p>0)的焦点F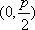
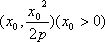
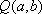
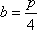

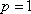

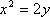
(2)假设存在点M,使得直线MQ与抛物线C相切于点M,
而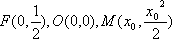
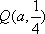
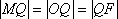
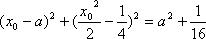
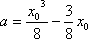
由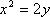
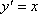
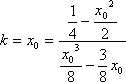
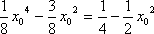
即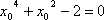
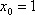
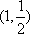
(3)若点M的横坐标为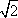
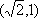
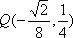
由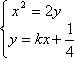
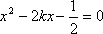
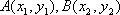
圆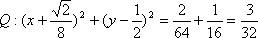
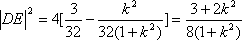
于是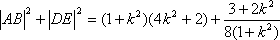
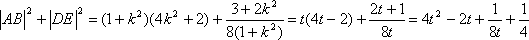
设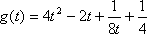
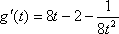
当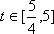
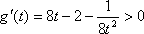
即当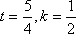
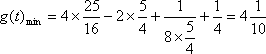
故当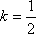
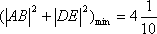
知识点
在直角坐标系xOy中,曲线






(1)求曲线
(2)设









正确答案
见解析
解析
(1)解法1 :设M的坐标为

易知圆



化简得曲线

解法2 :由题设知,曲线






(2)当点P在直线





整理得

设过P所作的两条切线



由

设四点A,B,C,D的纵坐标分别为

同理可得

于是由②,④,⑤三式得

所以,当P在直线
知识点
如图,椭圆C:


(1)求椭圆C的方程;
(2)AB是经过右焦点F的任一弦(不经过点P),设直线AB与直线l相交于点M,记PA,PB,PM的斜率分别为k1,k2,k3.问:是否存在常数λ,使得k1+k2=λk3?若存在,求λ的值;若不存在,说明理由。
正确答案
(1) 
解析
(1)由P

依题设知a=2c,则b2=3c2,②
②代入①解得c2=1,a2=4,b2=3.
故椭圆C的方程为
(2)方法一:由题意可设AB的斜率为k,
则直线AB的方程为y=k(x-1),③
代入椭圆方程3x2+4y2=12并整理,得(4k2+3)x2-8k2x+4(k2-3)=0.
设A(x1,y1),B(x2,y2),则有
x1+x2=

在方程③中令x=4得,M的坐标为(4,3k)。
从而


注意到A,F,B共线,则有k=kAF=kBF,即有
所以k1+k2=

④代入⑤得k1+k2=
又k3=
故存在常数λ=2符合题意。
(2)方法二:设B(x0,y0)(x0≠1),则直线FB的方程为:
令x=4,求得M
从而直线PM的斜率为
联立
得A
则直线PA的斜率为:

所以k1+k2=
故存在常数λ=2符合题意
知识点
在平面直角坐标系





(1)设动点P满足
(2)设
(3)设
正确答案
见解析。
解析
(1)设点P(x,y),则:F(2,0)、B(3,0)、A(-3,0)。
由


故所求点P的轨迹为直线
(2)将




直线MTA方程为:

直线NTB 方程为:

联立方程组,解得:
所以点T的坐标为
(3)点T的坐标为
直线MTA方程为:

直线NTB 方程为:

分别与椭圆

解得:

(方法一)当
令

当

所以直线MN必过x轴上的一定点D(1,0)。
(方法二)若



此时直线MN的方程为
若


直线ND的斜率

因此,直线MN必过
知识点
如图,已知椭圆








(1)求椭圆和双曲线的标准方程;
(2)设直线




(3)是否存在常数


正确答案
见解析。
解析
(1)设椭圆的半焦距为


所以 

又

故椭圆的标准方程为
由题意设等轴双曲线的方程
因此 双曲线的标准方程为
(2)设
则 
因为 点


因此 
即 
(3)由于


由根与系数的关系得
所以

同理可得
则 
又 
所以 
故
因此 存在

知识点
如图,F1,F2分别是双曲线C:
正确答案
解析
如图:|OB|=b,|O F1|=c,∴kPQ=

直线PQ为:y=










令y=0得:xM=



知识点
如图,







正确答案
解析
由已知得



知识点
如图,椭圆C:


(1)求椭圆C的方程;
(2) 求
正确答案
(1) 

解析
(1)由题:
左焦点(﹣c,0)到点P(2,1)的距离为:
由(1) (2)可解得:
∴所求椭圆C的方程为:
(2)易得直线OP的方程:y=

∵A,B在椭圆上,
∴
设直线AB的方程为l:y=﹣
代入椭圆:
显然
∴﹣

由上又有:


∴|AB|=



∵点P(2,1)到直线l的距离为:
∴S



当|m+2|=


此时直线l的方程y=﹣
知识点
扫码查看完整答案与解析