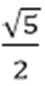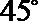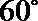- 圆锥曲线的综合问题
- 共478题
已知椭圆






(1)求该椭圆的方程;
(2)设椭圆的另一个焦点为






正确答案
见解析
解析
解:(1)抛物线


∴ 
又椭圆截抛物线的准线

∴ 得上交点为

由①代入②得


从而
∴ 该椭圆的方程为该椭圆的方程为
(2)∵ 倾斜角为


∴ 直线

由(1)知椭圆的另一个焦点为




解得

又







知识点
20.已知椭圆C:+=1(a>b>0)的离心率为,短轴一个端点到右焦点的距离为。
(1)求椭圆C的方程;
(2)设直线l与椭圆C交于A、B两点,坐标原点O到直线l的距离为,求△AOB面积的最大值。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知双曲线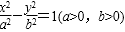
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知椭圆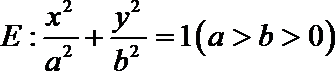
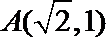

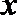
(Ⅰ)求椭圆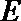
(Ⅱ)过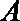

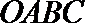
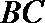
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知左焦点为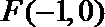

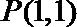
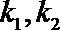
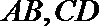
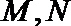
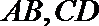
(1)求椭圆的标准方程;
(2)若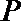
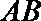
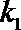
(3)若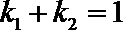
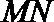
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知椭圆
(1)求椭圆E的方程;
(2)若M,N是直线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 已知双曲线



(Ⅰ)如果椭圆

(Ⅱ)如果椭圆




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆




(1)(ⅰ)若圆

(ⅱ)若椭圆上存在点


(2)设直线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆C:

(1)求椭圆的方程;
(2)设







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 函数的图象与方程的曲线有着密切的联系,如把抛物线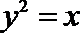
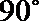
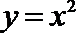
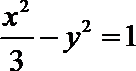
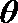
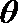
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析