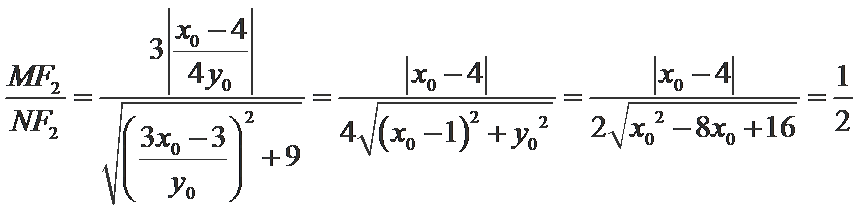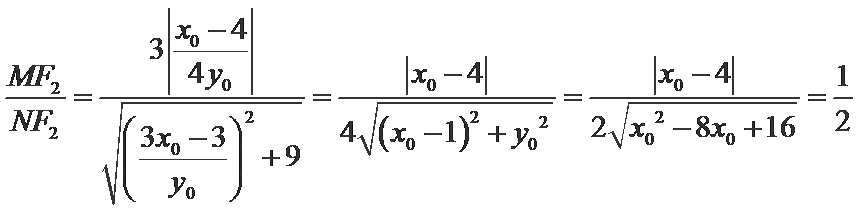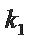- 圆锥曲线的综合问题
- 共478题
20.设圆
(I)证明
(II)设点E的轨迹为曲线C1,直线l交C1于M,N两点,过B且与l垂直的直线与圆A交于P,Q两点,求四边形MPNQ面积的取值范围.
正确答案
知识点
18.如图,在平面直角坐标系








(1)若圆



(2)若
①求证:
②求
正确答案
(1)圆

解析
试题分析:本题属于直线与圆锥曲线的综合问题,题目的难度较大,(1)直接求圆心和半径(2)证明定值问题时,要先表示出来,再通过计算化简得到(3)
(1)因为椭圆



从而圆

(2)①因为圆


即
同理,有
所以

从而
②设点

解得
同理,
所以




考查方向
解题思路
本题考查直线与圆锥曲线的位置关系,解决直线与椭圆的位置关系的相关问题时,常规思路是先把直线与椭圆联立方程组,消元、化简,然后应用根与系数的关系代入化简,从而解决相关问题。
易错点
1、第二问中证明
2、第三问中求
知识点
已知点






23.求动点

24.已知圆








正确答案

解析
设

考查方向
解题思路
第一问利用向量数量积的坐标运算直接求出抛物线的方程;
易错点
求不出
正确答案
解析
设



令

不妨设

①

②


综上,

考查方向
解题思路
第二问首先设出



易错点
求不出
已知Q为椭圆C:

23.求椭圆C的方程:
24.若直线l:y=kx+m(|k|≤
正确答案
(1)
解析
(1)因为




由题设可知

又点




①②联立解得,

故所求椭圆的方程为
考查方向
解题思路
(1)通过

易错点
线段OM的中点与线段AB的中点重合的转化
正确答案
(2)
解析
(2)设



由


由(1)-(2),得
由线段



又

把(4)(5)(6)代入(3)整理,得
于是由


所以
因为


所以


考查方向
解题思路
(1)通过

易错点
线段OM的中点与线段AB的中点重合的转化
抛物线C的方程为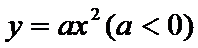
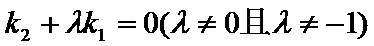
24.求抛物线C的焦点坐标和准线方程;
25.设直线AB上一点M,满足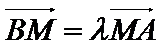
26.当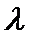
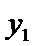
正确答案
(1)焦点坐标为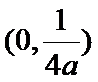
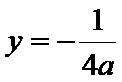
解析
(Ⅰ)由抛物线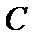
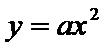
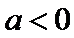
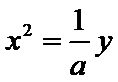
焦点坐标为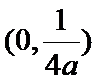
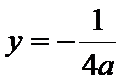
考查方向
解题思路
根据抛物线的几何性质直接得到即可;
易错点
无
正确答案
(2)略;
解析
(Ⅱ)证明:设直线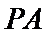
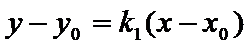
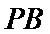
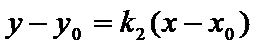
点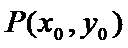
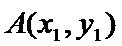
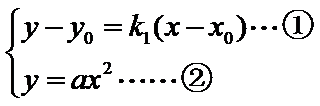
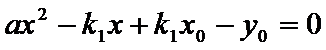
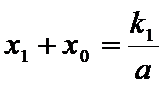
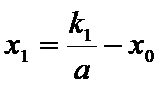
又点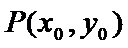
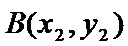
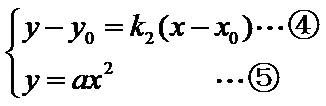
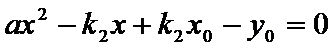
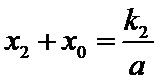
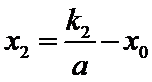
由已知得,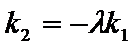
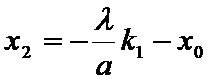
设点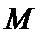
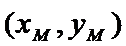
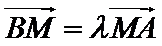
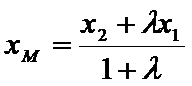
将③式和⑥式代入上式得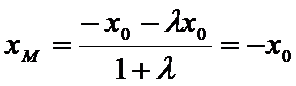
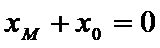
∴线段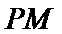
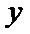
考查方向
解题思路
1
先根据条件求出A,B的横坐标后带入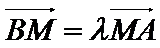
易错点
不会求解点A,B的坐标,运算量大;
正确答案
(3)
解析
(Ⅲ)因为点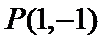
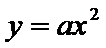
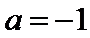
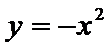
由③式知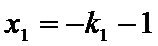
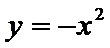
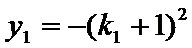
将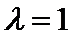
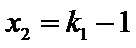
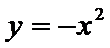
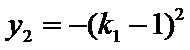
因此,直线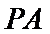
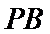
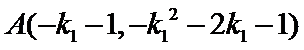
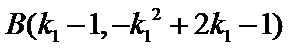
于是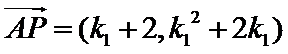
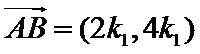
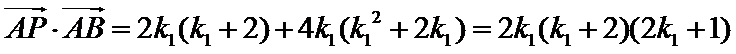
因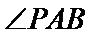
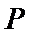
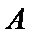
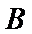
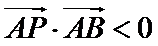
求得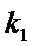
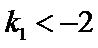
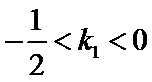
又点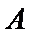
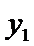
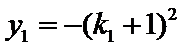
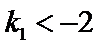
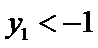
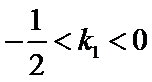
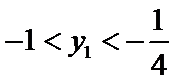
考查方向
解题思路
先求出抛物线的方程,然后根据第(2)问求出点A,B的坐标,然后将∠PAB为钝角转化为向量求解即可。
易错点
不会转化题中给出的条件∠PAB为钝角,导致做不出正确答案。
已知椭圆离心率为,左、右焦点分别为

26.求椭圆的方程;
27.若直线



正确答案
解析
(Ⅰ) 设

考查方向
解题思路
由椭圆的离心率得到a,c的关系,再由

易错点
注意椭圆中a,b,c三者的关系,和双曲线的区别.
正确答案
解析
当直线l斜率存在时:设

得: 
所以
所以
因为

当直线l斜率不存在时:
所以
综上:
解题思路
当直线l斜率不存在时,用坐标分别表示出


下列选项中对民事法律关系的表述正确的是( )。
A.鲁宾孙漂流到无人岛上后,通过劳动逐渐积攒起粮食、牲畜等物资,他在无人岛上主要形成以所有权为主的法律关系
B.甲男和乙女同居期间,两人约定乙女服用避孕药避孕,之后乙女擅自停服避孕药,并导致怀孕,且执意生下孩子,违反了甲、乙的约定,且侵犯了甲男的生育权,构成违约和侵权的竞合
C.A市工商局某科长甲在职务范围内,以工商局的名义向该市B银行贷款500万元,二者之间形成民事法律关系
D.甲发现乙和丙都有其需要的建材,就先跟丙接触,商谈此事。丙通知甲在下午两点前将为甲保留建材。后甲又约乙一点会谈,乙快两点才赴约,且当甲提出此事,即需要购买乙的建材时,乙称早已卖出,导致甲丧失了与丙订约的机会,甲和乙之间成立民事法律关系
正确答案
C
解析
[考点] 民事法律关系的判断[解析] 民事法律关系是指具体民事主体间发生的、符合民法的规定、具有民事权利义务内容的法律关系。 首先,民事法律关系作为法律关系的一种,是人与人之间的关系,并不因为它反映物的占有和交换而成为人与物的关系或物与物的关系。民事法律关系首先存在于两个或多个民事主体之间,如合同关系和侵权关系,其次,民事法律关系也存在于一方主体与对此负有消极不作为义务的其他主体之间,如所有权法律关系。因此,尽管所有权包含了人对物的关系,但其实质仍然是人与人之间的法律关系。在选项A中,“鲁宾孙漂流到无人岛上后”,尽管他“通过劳动逐渐积攒起粮食、牲畜等物资”,但由于在“无人岛”没有其他民事主体,民事法律关系无从产生,他在无人岛上不能形成任何法律关系。因此,选项A是错误的。 合同作为民事法律关系的一种,是一种旨在发生债权债务关系的合意,其目的在于产生、变更或者消灭某种财产权利义务关系,不具备此目的的,不属于合同法律关系的范畴。对此,《合同法》第2条第2款明确规定:婚姻、收养、监护等有关身份关系的协议,适用其他法律的规定。因此,在选项B中,“甲男和乙女同居期间,两人约定乙女服用避孕药避孕”,其约定对象属于典型的身份关系,不具有通常意义上合同的目的,不是合同。“之后乙女擅自停服避孕药,并导致怀孕,且执意生下孩子,违反了甲、乙的约定”,也不是违约行为。另一方面,根据《中华人民共和国妇女权益保障法》第51条的规定,妇女有按照国家有关规定生育子女的权利,也有不生育的自由。因此,女性具有自主决定是否生育的权利,“乙女擅自停服避孕药,并导致怀孕,且执意生下孩子”符合法律的规定,没有侵犯他人的权利,不是侵权行为。因此,选项B认为“乙女侵犯了甲男的生育权”也是错误的。综上所述,选项B不应当选。 在选项C中,“A市工商局某科长甲在职务范围内,以工商局的名义”,说明甲实施的行为是职务行为,即行为的一方当事人为A市工商局;“向该市B银行贷款500万元”,说明A市工商局与银行之间形成借贷合同法律关系,根据《合同法》第196条的规定,借贷法律关系作为一种合同,是指借款人向贷款人借款,到期返还借款并支付利息的合同,是典型的民事法律关系。因此,在这种法律关系中,政府机关 A市工商局与银行是平等的民事主体,二者之间形成民事法律关系,选项C是正确的。与此相类似的诸如政府机关食堂到菜市场上购买食物、用品等行为,都形成民事法律关系,应该与其行政行为相区别。 选项D描述的情形类似《合同法》中缔约过失的规定,即在订立合同过程中,一方有违背诚实信用原则的行为,给对方造成损失的,应当承担损害赔偿责任。在题中,表面上甲因为与乙的会谈导致其丧失了与丙的交易机会,但仔细分析可以看出,在甲与乙见面后,甲才提出“需要购买乙的建材”,显露缔约意向。因此,可以由此推测之前甲跟乙约定的会谈是生活会谈,并不具有法律上的意义,不是订约行为。因此,甲和乙之间的关系与朋友之间约定共进晚餐的行为性质相同,不属于法律关系的范畴。选项D不应当选。
18. 平面直角坐标系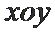
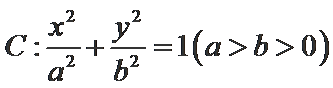
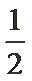
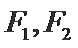
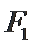
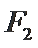
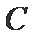
(1)求椭圆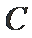
(2)过椭圆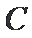
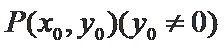
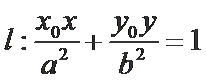
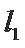
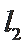
①设直线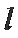
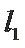
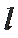

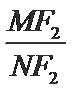
②若连接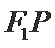
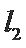
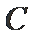
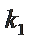
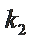
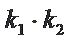
正确答案
见解析
解析
(1)由题意知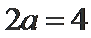
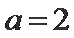
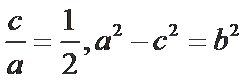
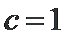
所以椭圆C的标准方程为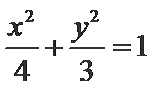
(2)①M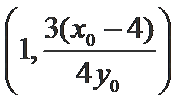
②点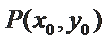
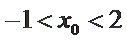
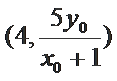
∵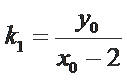
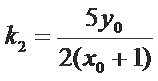
∴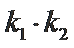
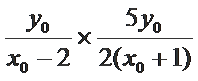

∵点P在椭圆C上, ∴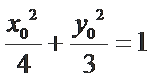
∴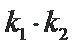
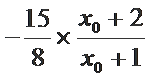
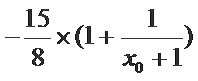
∵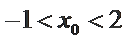
∴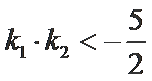
∴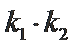
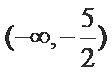
考查方向
解题思路
本题考查导数的性质,解题步骤如下:
(1)根据离心率和几何特点,求出椭圆方程
(2)表示M,N进而得
(3)表示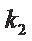
易错点
点M,N表示不当
知识点
如图,在平面直角坐标系xoy中,椭圆

26.求椭圆的方程;
27.若直线AB斜率为1时,求弦AB长;
28.过椭圆的对称中心O,作直线L,交椭圆与M,N,三角形FMN是否存在在大面积?若存在,求出它的最大面积值。若不存在,说明理由
正确答案
当AB的斜率为0时,AB=半长轴,即
2a=4,a=2;
又因为 e=c/a,
又
所以解析式为
解析
看解题步骤
考查方向
圆锥曲线
解题思路
利用离心率公式。abc之间的关系
易错点

教师点评
考查圆锥曲线解析式求解
正确答案
联立直线与椭圆方程得:5x2-8x=0设方程根为x1=0,x2=8/5,
|AB|=
解析
见答案
考查方向
直线与圆锥曲线的关系,两点之间的距离
解题思路
先求出两焦点的横坐标,利用距离与斜率、求两点间的距离公式求解
易错点
无
教师点评
考查了直线与圆锥曲线的关系,和用斜率求两点距离
正确答案
S⊿FMN= 

21.一种作图工具如图1所示.







(1)求曲线C的方程;
(2)设动直线





正确答案
21.(1)设点



所以
即
由于当点


于是



即所求的曲线
(2)(1)当直线




(2)当直线

由


因为直线

所以

又由


由原点




将①代入②得,
当

当

因



当且仅当
所以当

综合(1)(2)可知,当直线

解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析