- 圆锥曲线的综合问题
- 共478题
已知椭圆





(1)求
(2)设斜率不为









正确答案
见解析
解析
解析:(1)设
和

且




(2)设直线






设切点







化简并整理得


知识点
如图,两条相交线段






(1)若


(2)探究:是否存在常数


正确答案
见解析
解析
(1)由
解得

因为

设

化简得
又


因为


(2)设






若存常数



①当



即
即
即
所以,存常数


②当

故,存常数


知识点
已知椭圆







(1)求椭圆
(2)求
(3)若



正确答案
见解析。
解析
(1)易知



故方程为
(2)证明:设





设

∴
=


故所求范围是
(3)由对称性可知N

直线AN:


∴直线

知识点
20.已知椭圆C:





(1)求椭圆方程;
(2)过椭圆的左顶点A作两条弦
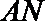






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知左焦点为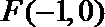

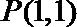
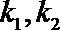
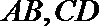
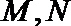
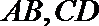
(1)求椭圆的标准方程;
(2)若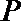
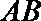
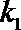
(3)若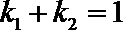
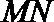
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知椭圆
(1)求椭圆E的方程;
(2)若M,N是直线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.给定椭圆






(1)求椭圆
(2)点






①当


②求证:
正确答案
(1)
所以,椭圆方程:
准圆方程:
(2)①易知
设直线为
联立
因为椭圆与直线有且只有一个交点,
所以
所以
②<ⅰ>当

设直线
由
同理,联立

由(*)(**)可知,


因此
<ⅱ>当

所以
解析
解析已在路上飞奔,马上就到!
知识点
22.已知抛物线





(1)求证:


(2)设


正确答案
解:(1)设直线的方程为:
联立方程可得

设





而

即


(2)由


即得:

由(1)中②代入得

解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆




(1)(ⅰ)若圆

(ⅱ)若椭圆上存在点


(2)设直线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.如图,已知抛物线














(1)求圆

(2)若


(3)过直线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析


































