- 函数模型及其综合应用
- 共70题
13.某食品的保鲜时间y(单位:小时)与储存温度x(单位:





正确答案
24
考查方向
易错点
1.没有发现192与48之间的关系导致不会解方程组;
知识点
建设项目的保修证书的主要内容包括( )。
A.保修时间
B.保修说明
C.保修单位的名称
D.保修所使用的材料
E.保修范围和内容
正确答案
A,B,C,E
解析
暂无解析
某山区外围有两条相互垂直的直线型公路,为进一步改善山区的交通现状,计划修建一条连接两条公路和山区边界的直线型公路,记两条相互垂直的公路为l1,l2,山区边界曲线为C,计划修建的公路为l,如图所示,M,N为C的两个端点,测得点M到l1,l2的距离分别为5千米和40千米,点N到l1,l2的距离分别为20千米和2.5千米,以l2,l1在的直线分别为x,y轴,建立平面直角坐标系xOy,假设曲线C符合函数y=
21.求a,b的值;
22.设公路l与曲线C相切于P点,P的横坐标为t.
①请写出公路l长度的函数解析式f(t),并写出其定义域;
②当t为何值时,公路l的长度最短?求出最短长度.
正确答案
解析
(1)由题意知,点M,N的坐标分别为(5,40),(20,2.5),
将其分别代入y=

解得
考查方向
解题思路
由题意知,点M,N的坐标分别为(5,40),(20,2.5),将其分别代入y=
易错点
本题考查利用数学知识解决实际问题,在实际应用问题时易错.
正确答案
t=10

解析
)①由(1)y=

∴y′=﹣
∴切线l的方程为y﹣

设在点P处的切线l交x,y轴分别于A,B点,则A(

∴f(t)=

②设g(t)=


t∈(5,10

从而t=10
∴g(t)min=300,
∴f(t)min=15
答:t=10

考查方向
解题思路
①求出切线l的方程,可得A,B的坐标,即可写出公路l长度的函数解析式f(t),并写出其定义域;
②设g(t)=
易错点
本题考查利用数学知识解键决实际问题,考查导数知识的综合运用,确定函数关系,在应用导数解题过程中易错.
某厂以x千克/小时的速度匀速生产某种产品(生产条件要求

(1)要使生产该产品1小时获得的利润不低于1200元,求x的取值范围;
(2)要使生产120千克该产品获得的利润最大,问:该厂应该选取何种生产速度?并求此最大利润.
正确答案
见解析
解析
知识点
某企业接到生产3000台某产品的A,B,C三种部件的订单,每台产品需要这三种部件的数量分别为2,2,1(单位:件),已知每个工人每天可生产A部件6件,或B部件3件,或C部件2件,该企业计划安排200名工人分成三组分别生产这三种部件,生产B部件的人数与生产A部件的人数成正比,比例系数为

(1)设生产A部件的人数为
(2)假设这三种部件的生产同时开工,试确定正整数
正确答案
见解析
解析
(1)设完成A,B,C三种部件的生产任务需要的时间(单位:天)分别为

期中
(2)完成订单任务的时间为




(i)当


由函数




故当

(ii)当






由函数



此时完成订单任务的最短时间大于
(iii)当





当


完成订单任务的最短时间为

综上所述,当
分别为44,88,68.
知识点
某工厂生产某种产品,每日的成本C(单位:元)与日产里x(单位:吨)满足函数关系式C=3+x,每日的销售额R(单位:元)与日产量x满足函数关系式
(1)求k的值;
(2)当日产量为多少吨时,毎日的利润可以达到最大,并求出最大值。
正确答案
见解析。
解析
解:(1)由题意可得:L=
因为x=2时,L=3
所以3=2×2+
所以k=18
(2)当0<x<6时,L=2x+
所以L=2(x﹣8)+


当且仅当2(8﹣x)=
当x≥6时,L=11﹣x≤5
所以当x=5时,L取得最大值6
所以当日产量为5吨时,毎日的利润可以达到最大值6。
知识点
若函数h(x)满足
①h(0)=1,h(1)=0;
②对任意a∈[0,1],有h(h(a))=a;
③在(0,1)上单调递减。
则称h(x)为补函数,已知函数
(1)判断函数h(x)是否为补函数,并证明你的结论;
(2)若存在m∈[0,1],使h(m)=m,称m是函数h(x)的中介元,记


(3)当λ=0,x∈(0,1)时,函数y=h(x)的图像总在直线y=1-x的上方,求p的取值范围。
正确答案
见解析
解析
(1)函数h(x)是补函数,证明如下:
①

②对任意a∈[0,1],有
③令g(x)=(h(x))p,有
=
因为λ>-1,p>0,所以当x∈(0,1)时,g′(x)<0,
所以函数g(x)在(0,1)上单调递减,故函数h(x)在(0,1)上单调递减。
(2)当

(ⅰ)当λ=0时,中介元
(ⅱ)当λ>-1且λ≠0时,
由(*)得


综合(ⅰ)(ⅱ),对任意的λ>-1,中介元为

当n无限增大时,

故对任意的n∈N+,

(3)当λ=0时,

(ⅰ)当0<p≤1时,

所以点(xp,h(xp))不在直线y=1-x的上方,不符合条件;
(ⅱ)当p>1时,依题意只须
即xp+(1-x)p<1在x∈(0,1)时恒成立,
设φ(x)=xp+(1-x)p,x∈[0,1],
则φ′(x)=p[xp-1-(1-x)p-1],
由φ′(x)=0得


又因为φ(0)=φ(1)=1,所以当x∈(0,1)时,φ(x)<1恒成立。
综上,p的取值范围是(1,+∞)。
知识点
已知
正确答案
解析



知识点
某工厂生产某种产品,已知该产品的月生产量

正确答案
见解析。
解析
每月生产x吨时的利润为
由
得当 
∴
故
答:每月生产200吨产品时利润达到最大,最大利润为315万元.
知识点
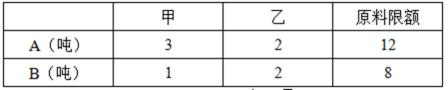
8.某企业生产甲乙两种产品均需用A,B两种原料,已知生产1吨每种产品需原料及每天原料的可用限额如表所示,如果生产1吨甲、乙产品
正确答案
解析
设每天生产甲乙两种产品分别为x,y顿,利润为z元,
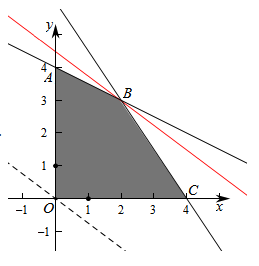
则3x+2y≤12x+2y≤8x≥0,y≥0, 目标函数为 z=3x+4y.
作出二元一次不等式组所表示的平面区域(阴影部分)即可行域。
由z=3, 即B的坐标为x=2,y=3,
∴Zmax=3x+4y=6+12=18.
即每天生产甲乙两种产品分别为2,3顿,能够产生最大的利润,最大的利润是18万元,
考查方向
本题主要考查应用题、线性规划最优解等知识,意在考查考生的理解问题解决问题的能力和数形结合的能力.
解题思路
设每天生产甲乙两=3x+4y得y=-34x+z4,
平移直线y=-34x+z4由图象可知当直线y=-34x+z4经过点B时,直线y=-34x+z4的截距最大, 此时z最大,
解方程组3x+2y=12x+2y=8,解得x=2y=分别为x,y顿,利润为z元,然后根据题目条件建立约束条件,得到目标函数,画出约束条件所表示的区域,然后利用平移法求出z的最大值.
易错点
1.不会根据题意设变量表示题中的约束条件;
2.不会利用线性规划求目标函数的最值。
教师点评
考生需要掌握目标函数的设立,了解约束条件并作图标,利用线性规划求目标函数的最值。
知识点
扫码查看完整答案与解析