- 函数模型及其综合应用
- 共70题
要测定古物的年代,常用碳的放射性同位素










(1) 求实数
(2) 测得湖南长沙马王堆汉墓女尸中
正确答案
(1)
(2)2100多年前
解析
(1)由题意可知,当


解得
(2)∵古墓中女尸
∴

解得
∴由此可推测古墓约是2100多年前的遗址。
知识点
某种商品每件进价12元,售价20元,每天可卖出48件,若售价降低,销售量可以增加,且售价降低

(1)试将该商品一天的销售利润表示成
(2)该商品售价为多少元时一天的销售利润最大?
正确答案
见解析
解析
(1)由题意可设,每天多卖出的件数为

又每件商品的利润为
∴该商品一天的销售利润为
(2)由
令

当


∴当商品售价为16元时,一天销售利润最大,最大值为432元
知识点
18.某房地产开发公司计划在一楼区内建造一个长方形公园





(1)若设休闲区的长和宽的比




(2)要使公园所占面积最小,休闲区
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 某地区预计明年从年初开始的前x个月内,对某种商品的需求总量

(1)写出明年第x个月的需求量
(2)如果将该商品每月都投放市场p万件,要保持每月都满足市场需求,则p至少为多少万件。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.某跨国饮料公司在对全世界所有人均GDP(即人均纯收入)在0.5千美元~8千美元的地区销售该公司
(1)下列几个模拟函数中




①
③

(2)若人均GDP为1千美元时,年人均


(3)因为



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,ABCD是正方形空地,边长为30m,电源在点P处,点P到边AD,AB距离分别为



(1)求S关于x的函数关系式及该函数的定义域;
(2)当x取何值时,液晶广告屏幕MNEF的面积S最小?
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 张家界某景区为提高经济效益,现对某一景点进行改造升级,从而扩大内需,提高旅游增加值,经过市场调查,旅游增加值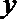
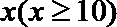
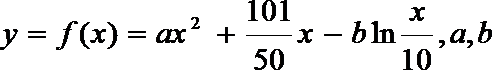
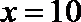
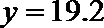
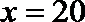
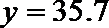
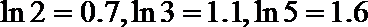
(1)求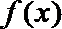
(2)求该景点改造升级后旅游利润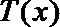
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.甲、乙两公司同时开发同一种新产品,经测算,对于函数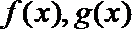
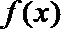
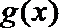
(1)试解释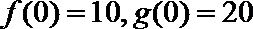
(2)设
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.为了加强环保建设,提高社会效益和经济效益,长沙市计划用若干时间更换一万辆燃油型公交车,每更换一辆新车,则淘汰一辆旧车,替换车为电力型和混合动力型车.今年初投入了电力型公交车128辆,混合动力型公交车400辆;计划以后电力型车每年的投入量比上一年增加50%,混合动力型车每年比上一年多投入a辆.
(1)求经过n年,该市被更换的公交车总数S(n);
(2)若该市计划7年内完成全部更换,求a的最小值.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.某工厂去年某产品的年产量为100万只,每只产品的销售价为10元,固定成本为8元.今年,工厂第一次投入100万元(科技成本),并计划以后每年比上一年多投入100万元(科技成本),预计产量年递增10万只,第n次投入后,每只产品的固定成本为


(1)求k的值,并求出
(2)问从今年算起第几年利润最高?最高利润为多少万元?
正确答案
(1)由
所以
(2)由

当且仅当
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析



















