- 直线、平面垂直的判定与性质
- 共668题
10.已知




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 箱子中有形状、大小都相同的3只红球和2只白球,先摸出1只球,记下颜色后放回箱子,然后再摸出1只球,则摸到两只不同颜色的球的概率为_____
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,在三棱柱




(Ⅰ)求证:
(Ⅱ)设





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知α,β表示两个不同的平面,m为平面α内的一条直线,则“α⊥β”是“m⊥β”的( )条件。(填“充分不必要”、“必要不充分”、“充要”或“既不充分也不必要”)
正确答案
必要不充分
解析
解析已在路上飞奔,马上就到!
知识点
16.在四棱锥P-ABCD中,∠ACD=90°,∠BAC=∠CAD,PA⊥平面ABCD,E为PD的中点。
(1)求证:平面PAC⊥平面PCD;
(2)求证:CE//平面PAB。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,已知四棱锥








(1)求证:
(2)当平面



正确答案
解:
(1)证明:∵





∵



∴

∴



且

(2)解法1:
由(1)知


又∵


又∵








从而


∴在等腰三角形







∴中位线




在




在




∴二面角

解法2:
由(1)知,以点


所在的直线分别为


设







则

设平面

则由
又





设平面

则由
又





∴二面角

解析
解析已在路上飞奔,马上就到!
知识点
16. 如图,四棱锥







(1)求证:

(2)




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.如图,在四棱锥









(1)求证:平面

(2)求平面

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.在多面体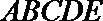
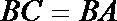
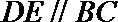
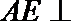
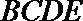
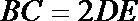
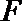
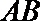
(I)求证: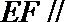
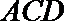
(II)若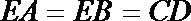
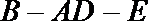
正确答案
证明:(Ⅰ)取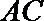
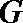
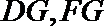
因为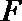
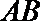
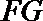
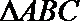
则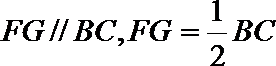
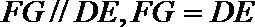
则四边形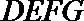
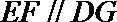
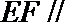
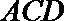
(Ⅱ)过点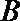
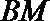
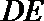
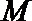
因为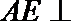
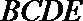
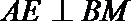
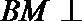
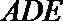
过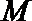
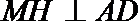

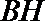
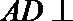
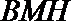
所以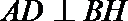
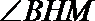
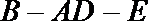
设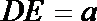
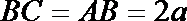
在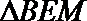
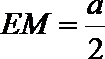
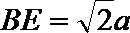
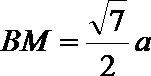
又因为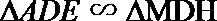
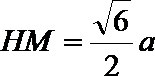
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析