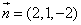- 直线、平面垂直的判定与性质
- 共668题
20.如图,在长方体



(1)求异面直线

(2)

正确答案
(1) 以




设





解二:三垂线定理;
解三:实在不会做就硬做
(2) 过











解二:或利用空间向量
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,在四棱锥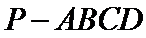
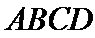
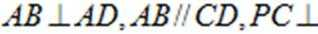
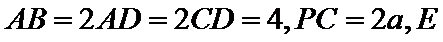

(Ⅰ)求证:平面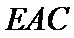

(Ⅱ)若二面角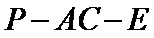
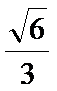
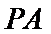
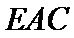
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 如图,在六面体










(Ⅰ)求证: 

(Ⅱ)求二面角
(Ⅲ) 求五面体
正确答案
解法一 向量法

则A(0,0,2),
B(2,0,2),C(0,1,2),E(2,0,0),
G(0,2,0),F(2,1,0)
(Ⅰ)
∴

故 BF//平面ACGD
(Ⅱ)

则


而平面ADGC的法向量
∴
故二面角D-CG-F的余弦值为
(Ⅲ)设DG的中点为M,连接AM.FM,
则
=



所以MF//DE,且MF=DE又∵AB//DE,且AB=DE
∴MF//AB,且MF=AB
∴四边形ABMF是平行四边形,即BF//AM,
又BF
(Ⅱ)由已知AD⊥面DEFG∴DE⊥AD ,DE⊥DG即DE⊥面ADGC ,
∵MF//DE,且MF=DE , ∴MF⊥面ADGC
在平面ADGC中,过M作MN⊥GC,垂足为N,连接NF,则
显然∠MNF是所求二面角的平面角.
∵在四边形ADGC中,AD⊥AC,AD⊥DG,AC=DM=MG=1


在直角三角形MNF中,MF=2,MN
∴




故二面角D-CG-F的余弦值为
(Ⅲ)

=

解析
解析已在路上飞奔,马上就到!
知识点
18.正方体













正确答案
解析
解析已在路上飞奔,马上就到!
知识点
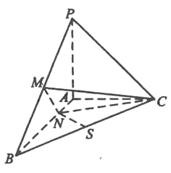
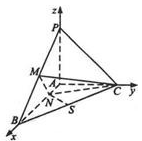
19.已知三棱锥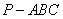
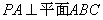
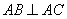
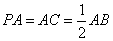
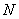
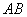
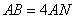
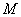
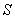
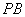
(1)求证: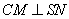
(2)求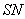
正确答案
设PA=1,以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立空间直角坐标系如图所示:
则P(0,0,1),C(0,1,0),B(2,0,0),M(1,0, ),N( ,0,0),S(1, ,0)
(1)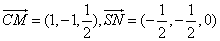
因为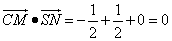
所以CM⊥SN
(2)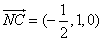
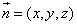
则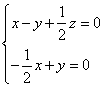
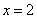
因为
所以SN与片面CMN所成角为45°。
解析
解析已在路上飞奔,马上就到!
知识点
18.如图, 






所成角为
(Ⅰ)求证:

(Ⅱ)求二面角
(Ⅲ)设点




正确答案
(Ⅰ)
证明: 因为


因为


从而

(Ⅱ)因为




即
所以



则




所以

设平面



令

因为




所以
因为二面角为锐角,所以二面角

(Ⅲ)点



因为


即

此时,点


解析
解析已在路上飞奔,马上就到!
知识点
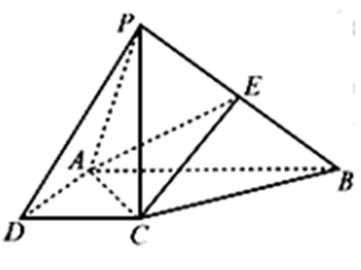
18. 如图所示, 四棱锥P-ABCD的底面是边长为1的正方形,PA⊥CD,PA = 1,PD=
(Ⅰ)求证:PA 
(Ⅱ)求二面角D-AC-E的余弦值;
(Ⅲ)在侧棱PC上是否存在一点F,使得BF // 平面AEC?若存在,指出F点的位置,并证明;若不存在,说明理由.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,在侧棱垂直于底面的四棱柱






(1)证明:
(2)证明:

(3)求

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,在直三棱柱




(Ⅰ)求证:

(Ⅱ)求二面角
(Ⅲ)试问线段





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,





(1)若



(2)求平面

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析