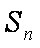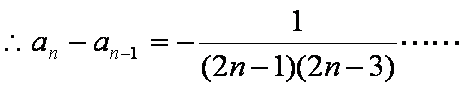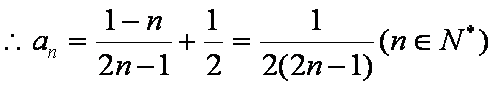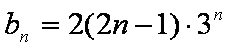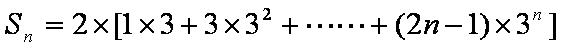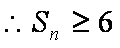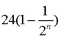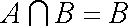- 错位相减法求和
- 共47题
已知数列





(1)求数列

(2)设




正确答案
见解析
解析
(1)

当



所以数列

(2)


知识点
已知数列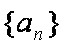
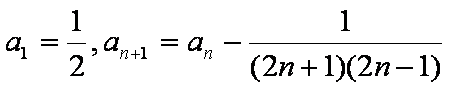
(1) 求数列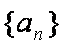
(2) 设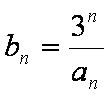
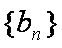

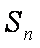
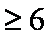
正确答案
见解析
解析
(1)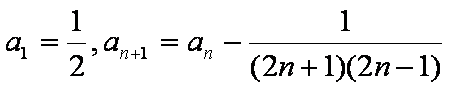

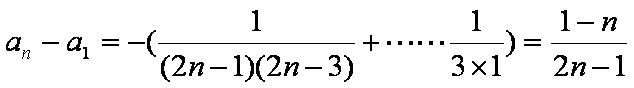
(2)又(1)知,
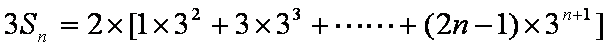
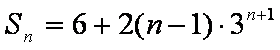
知识点
已知数列





(1)求数列

(2)设




正确答案
见解析
解析
(1)

当



所以数列

(2)


知识点
已知集合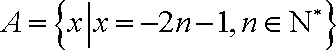
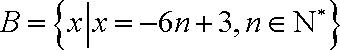
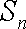
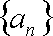
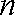
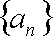
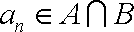
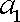

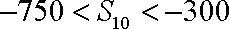
(1)求数列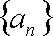
(2)若数列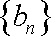
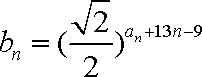
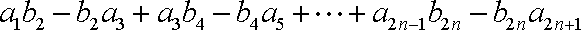
正确答案
(1)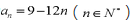
解析
解析:(1)由题设知: 集合
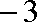
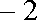
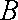
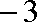
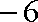
由此可得,对任意的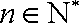

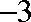
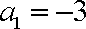
设等差数列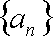
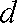
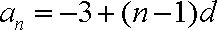
因为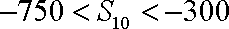
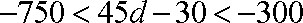
由于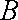
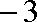
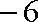
所以
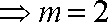
所以数列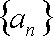
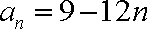
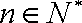
(2)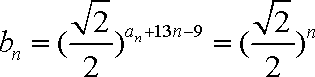
于是有
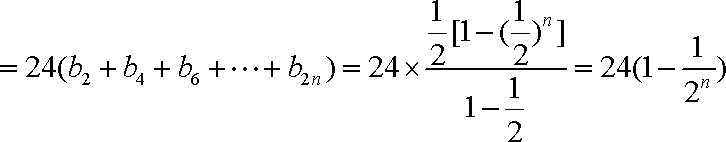
知识点
已知数列




(1)证明:数列
(2)求数列


正确答案
见解析
解析
解析:
(1) ∵



∴设

由上可知,数列

(2)由(1)知,

∴
即
令
则
②-①,得
∴
知识点
扫码查看完整答案与解析