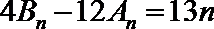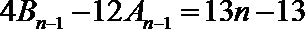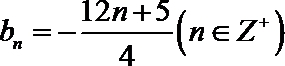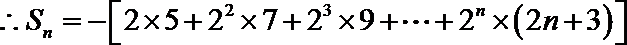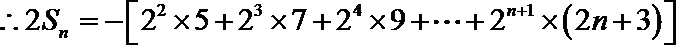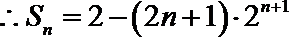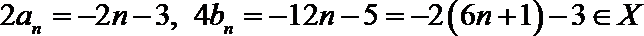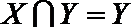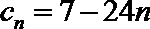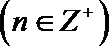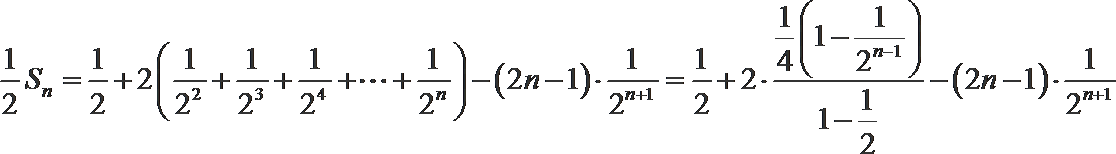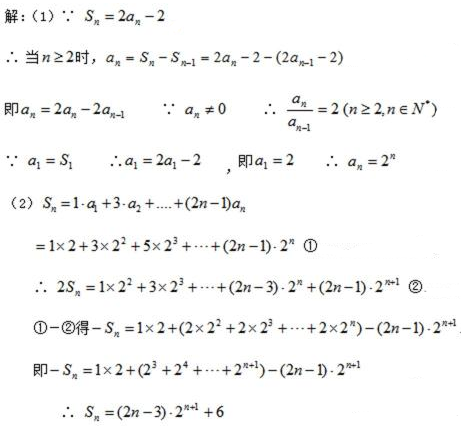- 错位相减法求和
- 共47题
22.若
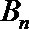
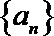
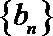
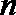
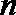
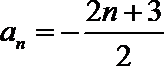
(1)求数列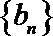
(2)设数列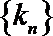
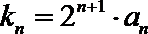
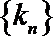
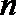
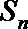
(3)设集合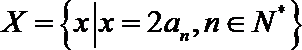
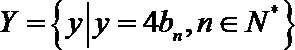
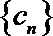
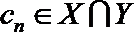
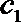


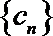
正确答案
(1)∵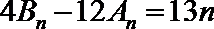
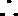
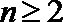
作差得: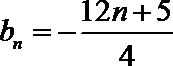
又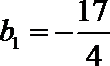
(2)
(3)对任意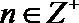
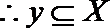
∵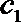
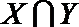
∴
设等差数列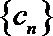
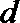
则
∵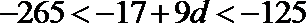
得
而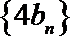
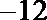
∴
∴
解析
解析已在路上飞奔,马上就到!
知识点
19.已知数列




(1)证明数列
(2)求通项


(3)设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 已知数列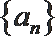


(1)求数列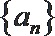
(2)设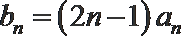
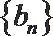
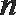
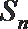
正确答案
解:(1)∵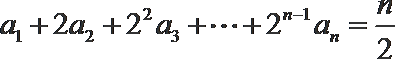
∴当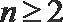
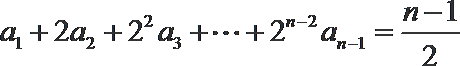
①-②得,

又∵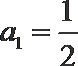
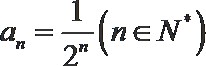
(2)由(1)知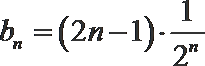
∴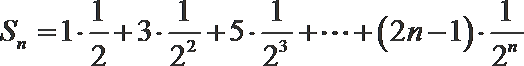
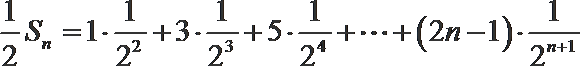
④-⑤得,
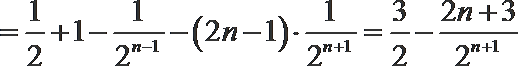
∴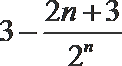
解析
解析已在路上飞奔,马上就到!
知识点
13.如图所示,将数以斜线作如下分群:(1),(2,3),(4,6,5),(8,12,10,7),(16,24,20,14,9),…,并顺次称其为第1群,第2群,第3群,第4群,…,
(1)第7群中的第2项是( );
(2)第n群中n个数的和是( ).
正确答案
(1)96
(2)3·2n-2n-3
解析
解析已在路上飞奔,马上就到!
知识点
16.已知数列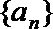

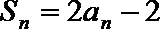
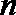
(1)求数列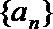
(2)记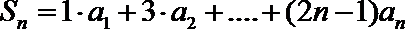
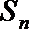
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知:对于数列




(1)若数列



(2)若数列

① 设

② 求:

正确答案
解:(1)依题意
(2)①由
∵


故


∴
∵
∴
∴

⑴-⑵得 
∴
解析
解析已在路上飞奔,马上就到!
知识点
6. 已知数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.数列




(1)求数列
(2)求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.各项都为正数的数列{an},满足a1=1,
(1)求数列{an}的通项公式;
(2)求数列
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知数列



(1)求数列
(2)数列



(3)设各项均不为零的数列






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析