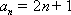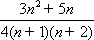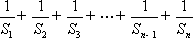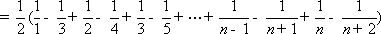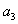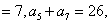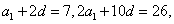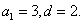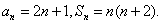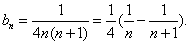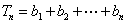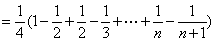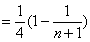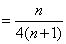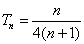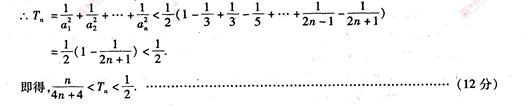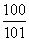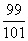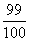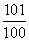- 裂项相消法求和
- 共41题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
已知公差不为0的等差数列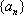

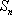
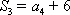
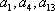

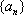
(2)求数列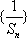

正确答案
(1)
(2)
解析
(1)设等差数列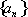
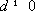
因为
所以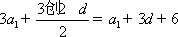
因为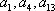
所以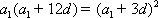
由①,②可得: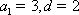
所以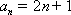
(2)由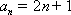
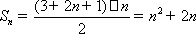
……………………………………9分
所以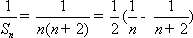
所以
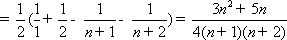
所以数列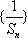

知识点
如图,


正确答案
5,
解析
首先由割线定理不难知道





知识点
已知等差数列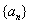
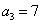
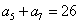
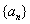
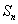
(1) 求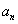
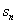
(2) 令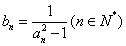
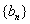
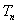
正确答案
见解析。
解析
(1)设等差数列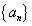
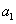
由于
所以
解得
由于
(2)因为 
因此
故
所以数列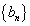
知识点
已知正项数列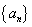
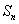
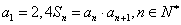
(1)求数列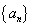
(2)设数列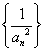

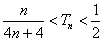
正确答案
见解析。
解析
知识点
已知等差数列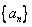
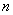
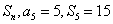
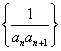
正确答案
解析
略
知识点
已知数列




(1)求数列
(2)数列



正确答案
(1)
(2)
解析
(1)



经检验
综上 
(2)由(1)可知
=
=
=
知识点
已知数列



(1)求数列
(2)令



正确答案
(1)
解析
解析: (1)因为

又

(2) 易得

所以
所以 
知识点
19. 已知数列



(1)求数列
(2)设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.将杨晖三角形中的每一个数


观察莱布尼兹三角形规律,计算极限
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析