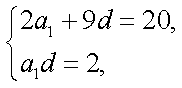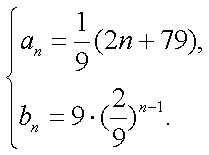- 错位相减法求和
- 共47题
19. 设等差数列
(I)求数列
(II)记

正确答案
(1)
(2)
解析
试题分析:本题属于数列应用中的基本问题,题目的难度是逐渐由易到难
(Ⅰ)设等差数列的




由题意可知:
所以

(Ⅱ)令
相减得

考查方向
解题思路
本题考查数列的性质,解题步骤如下:
1、利用基本量法求出通项;
2、利用错位相减法求和
易错点
第一问中的易计算出现问题。
知识点
21.在数列

(1)求数列
(2)求证:数列
(3)设数列



正确答案
(1)∵
∴数列{


∴
(2)∵
∴
∴
∴数列


(3)由(1)知,


∴
∴
于是

两式①-②相减得
=
∴
解析
解析已在路上飞奔,马上就到!
知识点
17.已知数列
(1)求数列
(2)求数列
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知数列{bn}的前n项和


(1) 求数列{an}和数列{bn}的通项公式;
(2) 若
正确答案
(1)当
又
∴
由
(2)
∵
∴ 
∴ {cn}的最大项为
∴
∴
∴ 实数m的取值范围为
解析
解析已在路上飞奔,马上就到!
知识点
7.设曲线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
根据《票据法》的规定,下列属于支票绝对应记载事项的有( )。
A.付款人名称
B.确定的金额
C.付款地
D.付款日期
正确答案
A,B
解析
[解析] 支票绝对应记载的事项有:(1)表明“支票”的字样;(2)无条件支付的委托;(3)确定的金额;(4)付款人名称;(5)出票日期;(6)出票人签章。支票上未记载前述六项规定事项之一的,则支票无效。
17.已知数列{an}的前n项和为Sn ,向量a= (S n ,1),b= (2n — 1, 


①求数列{bn}的通项公式,
②设Cn =
正确答案
(1)
(2)①
解析
(1)∵






(2)①∵








考查方向
数列的通项公式和求和
解题思路
(1)利用
(2)①利用

易错点
1、利用定义求通项公式
2、第二问中错位相减法计算的准确性;
知识点
18.设等差数列
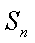
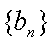

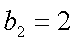
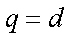
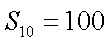
(1)求数列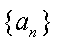
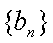
(2)当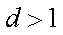
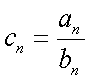
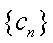
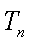
正确答案
(1)由题意有,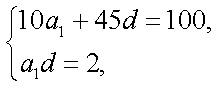
解得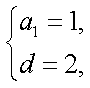
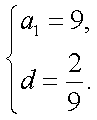
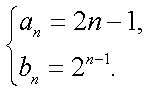
(2)由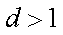
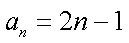
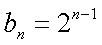
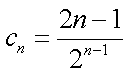
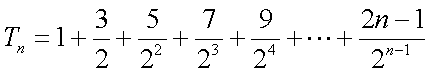
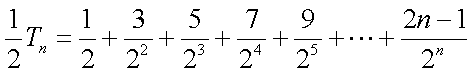
①-②可得
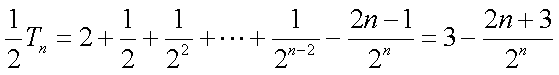
故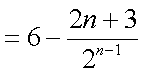
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析