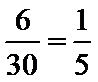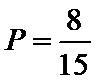- 随机事件的频率与概率
- 共77题
8.某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持续时间为40秒.若一名行人来到该路口遇到红灯 ,则至少需要等待15秒才出现绿灯的概率为( )
正确答案
解析
因为红灯持续时间为40秒.所以这名行人至少需要等待15秒才出现绿灯的概率为
考查方向
解题思路
对于几何概型的概率公式中的“测度”要有正确的认识,它只与大小有关,而与形状和位置无关,并与变量个数有关,在解题时,要掌握“测度”为长度、面积、体积、角度等常见的几何概型的求
易错点
读不懂题意错解为15/40错选c
知识点
11.某食堂规定,每份午餐可以在四种水果中任选两种,则甲、乙两同学各自所选的两种水果相同的概率为______.
正确答案
解析
从4种水果中选择2种,共有6种选法,甲乙挑选同一种水果的方法占其中1种,依据古典概型知概率为
考查方向
解题思路
古典概型
易错点
事件的个数
知识点
7.已知



正确答案
解析
试题分析:





























考查方向
解题思路
列举出所有的基本事件,再找出符合条件的基本事件,便可得解。
易错点
列举时,要注意不重不漏。
知识点
8.在区间





的概率,则
正确答案
解析
由题意知,事件“







考查方向
解题思路
转化为面积有关的几何概型分别计算出概率即可判断。
易错点
不会将其转化为面积有关的几何概型来做。
知识点
17. 人的体重是人的身体素质的重要指标之一.某校抽取了高二的部分学生,测出他们的体重(公斤),体重在40公斤至65公斤之间,按体重进行如下
(Ⅰ)求该校抽取的学生总数以及第2组的频率;
(Ⅱ)学校为进一步了解学生的身体素质,在第1
正确答案
(1)0.25;(2)
解析
试题分析:本题属于平率分布直方图及古典概型的应用,
(1)直接按照步骤来求;
(2)根据古典概型的公式来计算。
(Ⅰ)设该校抽查的学生总人数为n,第 2组、第3组的频率分别为

则



所以该校抽查的学生总人数为240人,从左到右第2组的频率为0.25
(Ⅱ)前3组的频率之比是1 : 2 : 3,则按照分层抽样,这6人的构成是第1组1人(不妨设为A),第2组2人(不妨设为



所以这2人来自同一组的概率
考查方向
解题思路
本题考查平率分布直方图及古典概型的应用,解题步骤如下:(1)直接按照步骤来求;根据古典概型的公式来计算。
易错点
误将图像的纵坐标当做频率。
知识点
18.某市小型机动车驾照“科二”考试中共有5项考察项目,分别记作①,②,③,④,⑤.
(1)某教练将所带10名学员“科二”模拟考试成绩进行统计(如表所示),并打算从恰有2项成绩不合格的学员中任意抽出2人进行补测(只测不合格的项目),求补测项目种类不超过3项的概率;
(2)如图,某次模拟演练中,教练要求学员甲倒车并转向90°,在汽车边缘不压射线AC与射
线BD的前提下,将汽车驶入指定的停车位. 根据经验,学员甲转向90°后可使车尾边缘完全落在线段CD,且位于CD内各处的机会相等.若CA=BD=0.3m, AB=2.4m. 汽车宽度为1.8m, 求学员甲能按教练要求
完成任务的概率。
正确答案
(1)
解析
试题分析:本题属于古典概型和几何概型的综合问题,(1)列表找出基本事件的总数,然后找到所求基本事件的个数,再利用古典概型公式即可解出;(2)利用几何概型的公式转化为线段的比值来求解。
(1)根据题意,学员(1),(2),(4),(6),(9)恰有两项不合格,从中任意抽出2人,所有情况如下:
由表可知,全部10种可能的情况中,有6种情况补测项数不超过

(2) 在线段CD上取两点





考查方向
解题思路
本题考查古典概型和几何概型的综合问题,解题步骤如下:(1)列表找出基本事件的总数,然后找到所求基本事件的个数,再利用古典概型公式即可解出;(2)利用几何概型的公式转化为线段的比值来求解。
易错点
第二问不知道转化为线段之比来解答。
知识点
13.袋中有形状、大小都相同的4个球,其中1个白球,1个红球,2个黄球。从中一次随机取出2个球,则这2个球颜色不同的概率为 .
正确答案
考查方向
解题思路
本题考查古典概型,解题步骤如下:
易错点
审题不清和考虑不全面导致出错。
知识点
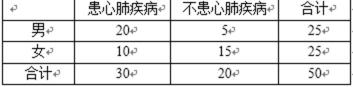
18. 近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重.大气污染可引起心悸、呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机对入院的50人进行了问卷调查得到了如下的列联表:
(Ⅰ)用分层抽样的方法在患心肺疾病的人群中抽6人,再从6人中选2人,求恰有一名女性的概率?
(Ⅱ)为了研究心肺疾病是否与性别有关,请计算出统计量K2,你有多大的把握认为心肺疾病与性别有关?
下面的临界值表供参考:
正确答案
(1)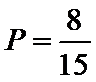
解析
试题分析:本题属于考查了分层抽样和古典概型以及独立性检验,(1)先利用分层抽样的方法计算出男女各抽多少人,然后利用古典概型公式计算;(2)利用独立性检验的方法来解(Ⅰ)解:在患心肺疾病人群中抽6人,则抽取比例为
∴ 女性应该抽取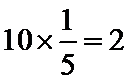
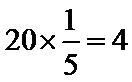
女性2人记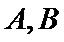
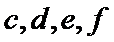
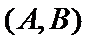
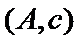
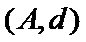
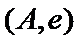

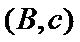
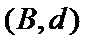
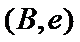
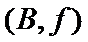
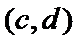
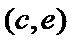
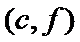
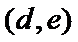
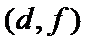
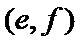
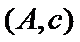
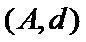
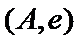
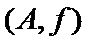
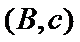
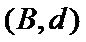
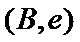
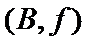
故上述抽取的6人中选2人,恰有一名女性的概率概率为
(Ⅱ):∵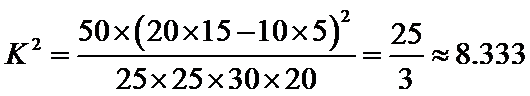
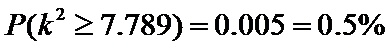
那么,我们有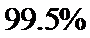
考查方向
解题思路
本题考查古典概型和独立性检验,解题步骤如下:(1)先利用分层抽样的方法计算出男女各抽多少人,然后利用古典概型公式计算;(2)利用独立性检验的方法来解。
易错点
分类容易遗漏。
知识点
18.某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到图3所示茎叶图,对不低于75
(Ⅰ)根据以上资料完成下面的2×2列联表,若据此数据算得
附:
(Ⅱ) 估计用户对该公司的产品“满意”的概率;
(Ⅲ) 该公司为对客户做进一步的调查,从上述对其产品满意的用户中再随机选取2人,求这两人都是男用户或都是女用户的概率.
正确答案
(1)在犯错的概率不超过5%的前提下,不能认为“满意与否”与“性别”有关
(2)
解析
解:(Ⅰ)
-----------------------------2分
∵
∴在犯错的概率不超过5%的前提下,不能认为“满意与否”与“性别”有关。-----------4分
(Ⅱ)因样本20人中,对该公司产品满意的有6人,故估计用户对该公司的产品“满意”的概率为
(Ⅲ)由(Ⅰ)知,对该公司产品满意的用户有6人,其中男用户4人,女用户2人,
设男用户分别为

从中任选两人,记事件A为“选取的两个人都是男用户或都是女用户”,则
总的基本事件为

而事件A包含的基本事件为
故
考查方向
解题思路


易错点
将茎叶图处理成列联表数据出错,在求
知识点
6.某中学有3个社团,每位同学参加各个社团的可能性相同,甲、乙两位同学均参加其中一个社团,则这两位同学参加不同社团的概率为( )
正确答案
解析
两个同学参加相同社团的概率为p=3/9=1/3,则所求事件的概率为1-1/3=2/3.
考查方向
解题思路
正难则反,可以先求出对立事件的概率,再用1减去这个概率值即可。
易错点
在找要求的事件个数容易漏解。
知识点
扫码查看完整答案与解析