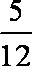- 随机事件的关系
- 共394题
如图,在边长为π的正方形内的正弦曲线
正确答案
解析
区域M的面积为:SM=



知识点
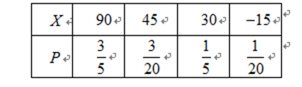
一次考试共有12道选择题,每道选择题都有4个选项,其中有且只有一个是正确的.评分标准规定:“每题只选一个选项,答对得5分,不答或答错得零分”.某考生已确定有8道题的答案是正确的,其余题中:有两道题都可判断两个选项是错误的,有一道题可以判断一个选项是错误的,还有一道题因不理解题意只好乱猜.请求出该考生:
(1) 得60分的概率;
(2) 所得分数ξ的分布列和数学期望.
正确答案
见解析。
解析
(1) 设“可判断两个选项是错误的”两道题之一选对的为事件A,“有一道题可判断一个选项是错误”选对的为事件B,“有一道题不理解题意”选对的为事件C,
∴P(A)= 



(2) ξ可能的取值为40,45,50,55,60………………………………5分
P(ξ=40)=
P(ξ=45)=
…………………………………………………………………………7分
P(ξ=50)=

P(ξ=55)=

P(ξ=60)=
…………………………………………………………………………10分
(3) Eξ=40×




知识点
某工厂生产A,B两种型号的玩具,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品,现随机抽取这两种玩具各100件进行检测,检测结果统计如下:
(1)试分别估计玩具A、玩具B为正品的概率;
(2)生产一件玩具A,若是正品可盈利40元,若是次品则亏损5元;生产一件玩具B,若是正品可盈利50元,若是次品则亏损10元,在(1)的前提下,
(i)记X为生产1件玩具A和1件玩具B所得的总利润,求随机变量X的分布列和数学期望;
(ii)求生产5件玩具B所获得的利润不少于140元的概率。
正确答案
见解析
解析
(1)玩具A为正品的概率约为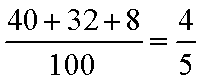
玩具B为正品的概率约为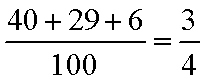
(2)解:(ⅰ)随机变量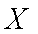
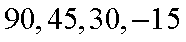
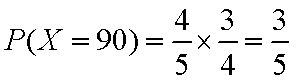
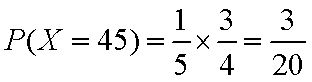
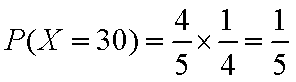
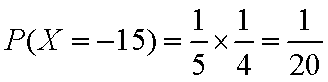
所以,随机变量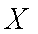
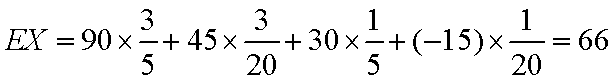
(ii)设生产的5件玩具B中正品有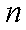
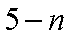
依题意,得 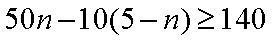
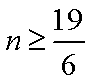
所以 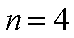
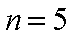
设“生产5件玩具B所获得的利润不少于140元”为事件
则 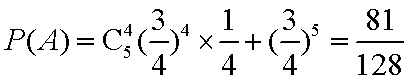
知识点
连续抛掷两枚骰子得到的点数分别是m、n,则向量a=(m,n)与向量b=(1,1)共线的概率是( )
正确答案
解析
由向量a=(m,n)与向量b=(1,1)共线,可得m=n,
连续抛掷两枚骰子到点数m,n的可能共有36种,m=n的有6种,分别是(1,1),(2,2),(3,3),(4,4),(5,5),(6,6),共6种,所以,所求概率为P=
知识点
某市职教中心组织厨师技能大赛,大赛依次设基本功(初赛)、面点制作(复赛)、热菜烹制(决赛)三个轮次的比赛,已知某选手通过初赛、复赛、决赛的概率分别是


(1)设该选手参赛的轮次为

(2)对于(I)中的

正确答案
见解析。
解析
(1)
记“该选手通过初赛”为事件A,“该选手通过复赛”为事件B,




(2)当

当

当

∴事件D发生的概率是
知识点
扫码查看完整答案与解析