- 随机事件的关系
- 共394题
某班联欢会举行抽奖活动,现有六张分别标有1,2,3,4,5,6六个数字的形状相同的卡片,其中标有偶数数字的卡片是有奖卡片,且奖品个数与卡片上所标数字相同,游戏规则如下:每人每次不放回抽取一张,抽取两次。
(1)求所得奖品个数达到最大时的概率;
(2)记奖品个数为随机变量

正确答案
见解析
解析
(1)由题意可知所得奖品个数最大为10,概率为:
(2)

所以
知识点
期末考试结束后,随机抽查了某校高三(1)班5名同学的数学与物理成绩,如下表:
(1)分别求这5名同学数学与物理成绩的平均分与方差,并估计该班数学与物理成绩那科更稳定。
(2)从4名数学成绩在90分以上的同学中选2人参加一项活动,以X表示选中同学的物理成绩高于90分的人数,求随机变量X的分布列及数学期望E(X)的值。
正确答案
见解析
解析
(Ⅰ)5名学生数学成绩的平均分为:
5名学生数学成绩的方差为:
5名学生物理成绩的平均分为:
5名学生物理成绩的方差为:
因为样本的数学成绩方差比物理成绩方差大,所以,估计高三(1)班总体物理成绩比数学成绩稳定.
(2)由题意可知,

随机变量
知识点








某城市环保局从该市市区


(1)从这

(2)从这



(3)根据这


正确答案
见解析
解析
(1)从茎叶图可知,空气质量为一级的有4天,为二级的有6天,超标的有5天
记“从

则
(2)




所以
…………………………………9分

(3)


所以估计一年中有
(说明:答243天,244天不扣分)
知识点
将一颗骰子掷两次,观察出现的点数,并记第一次出现的点数为m,第二次出现的点数为n,向量




正确答案
解析
略
知识点
某超市在节日期间进行有奖促销,凡在该超市购物满300元的顾客,将获得一次摸奖机会,规则如下:
奖盒中放有除颜色外完全相同的1个红球,1个黄球,1个白球和1个黑球,顾客不放回的每次摸出1个球,若摸到黑球则停止摸奖,否则就要将奖盒中的球全部摸出才停止,规定摸到红球奖励10元,摸到白球或黄球奖励5元,摸到黑球不奖励。
(1)求1名顾客摸球3次停止摸奖的概率;
(2)记X为1名顾客摸奖获得的奖金数额,求随机变量X的分布列和数学期望。
正确答案
见解析
解析
(1)解:设“1名顾客摸球3次停止摸奖”为事件A,
则 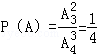
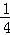
(2)解:随机变量X的所有取值为0,5,10,15,20.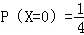
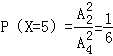
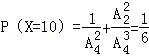
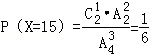
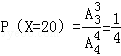
所以,随机变量X的分布列为:
知识点
某大楼共有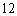
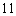
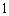
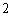
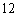
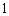
特殊原因,电梯只允许停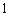
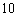
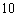
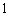
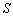
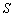
正确答案
解析
略
知识点
甲,乙,丙三位学生独立地解同一道题,甲做对的概率为





(1) 求至少有一位学生做对该题的概率;
(2) 求

(3) 求
正确答案
见解析。
解析

(1)由于事件“至少有一位学生做对该题”与事件“

(2)由题意知

整理得 

由


(3)由题意知



∴


知识点
某校高三年级同学进行体育测试,测试成绩分为优秀、良好、合格三个等级,测试结果如下表:(单位:人)
按优秀、良好、合格三个等级分层,从中抽取

(1) 求
(2) 若用分层抽样的方法,在合格的同学中按男女抽取一个容量为



正确答案
见解析
解析
(1)设该年级共


则
(2)依题意,






知识点
某工厂甲、乙两个车间包装同一种产品,在自动包装传送带上每隔一小时抽一包产品,称其重量(单位:克)是否合格,分别记录抽查数据,获得重量数据茎叶图(如下).
(1)根据样本数据,计算甲、乙两个车间产品重量的均值与方差,并说明哪个车间的产品的重量相对稳定;
(2)若从乙车间6件样品中随机抽取两件,求所抽取两件样品重量之差不超过2克的概率。
正确答案
见解析
解析
(1)设甲、乙两个车间产品重量的均值分别为







由于 
(2)从乙车间6件样品中随机抽取两件,结果共有15个:


设所抽取两件样品重量之差不超过2克的事件为A,则事件A共有4个结果:

所以 
知识点
在一次抽奖活动中,有甲、乙等6人获得抽奖的机会。抽奖规则如下:主办方先从6人中随机抽取两人均获奖1000元,再从余下的4人中随机抽取1人获奖600元,最后还从这4人中随机抽取1人获奖400元。
(1)求甲和乙都不获奖的概率;
(2)设X是甲获奖的金额,求X的分布列和均值
正确答案
见解析
解析
(1)设“甲和乙都不获奖”为事件A , ………………………………………1分
则P(A)=
答:甲和乙都不获奖的概率为
(2)X的所有可能的取值为0,400,600,1000,…………………………………………………6分
P(X=0)=


P(X=1000)=
∴X的分布列为
…………………………………11分
∴E(X)=0×



答: 甲获奖的金额的均值为500(元). ……………………………………………………………13分
知识点
扫码查看完整答案与解析