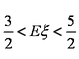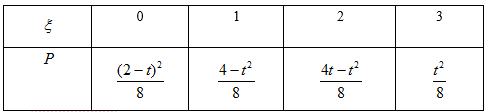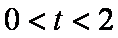- 随机事件的关系
- 共394题
某学校对高三学生一次模拟考试的数学成绩进行分析,随机抽取了部分学生的成绩,得到如图所示的成绩频率分布直方图。
(1)根据频率分布直方图估计这次考试全校学生数学成绩的众数、中位数和平均值;
(2)若成绩不低于80分为优秀成绩,视频率为概率,从全校学生中有放回的任选3名学生,用变量ξ表示3名学生中获得优秀成绩的人数,求变量ξ的分布列及数学期望E(ξ) 。
正确答案
(1)众数:75,中位数:75,平均值为74.6
(2)E(ξ)=
解析
(1)依题意可知,
众数:75,中位数:75,

所以综合素质成绩的的平均值为74.6。
(2)由频率分布直方图知优秀率为
由题意知ξ
故其分布列为

知识点
一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4。
(1)从袋中随机抽取两个球,求取出的球的编号之和不大于
(2)先从袋中随机取一个球,该球的编号为


正确答案
(1)
解析
(1)从袋子中随机取两个球,其一切可能的结果组成的基本事件有1和2,1和3,1和4,2和3,2和4,3和4,共6个
从袋中随机取出的球的编号之和不大于4的事件有1和2,1和3两个
因此,所求事件的概率是
(2)先从袋中取出一个球,记下编号为



















满足条件




所以,所求的概率为
知识点
一排9个座位坐了3个三口之家,若每家人坐在一起,则不同的坐法种数为
正确答案
解析
此排列可分两步进行,先把三个家庭分别排列,每个家庭有



知识点
现有甲、乙、丙三人参加某电视台的应聘节目非你莫属,若甲应聘成功的概率为 ,乙、丙应聘成功的概率均为(0<t<2),且三个人是否应聘成功是相互独立的。
(1)若乙、丙有且只有一个人应聘成功的概率等于甲应聘成功是相互独立的,求t的值;
(2)记应聘成功的人数为ξ,若当且仅当ξ为2时概率最大,求E(ξ)的取值范围。
正确答案
(1)t=1(2)
解析
解析:(1)由题意得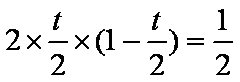
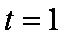
(2)
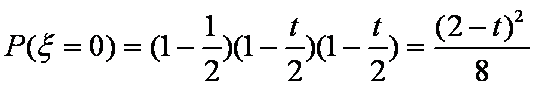
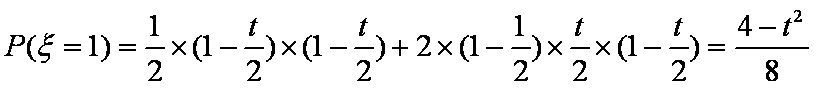
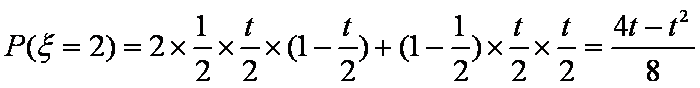
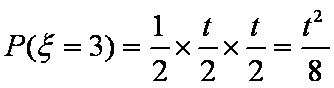
故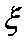
……………………7分
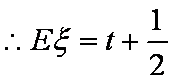
由题意得: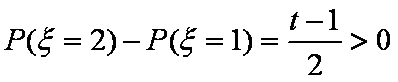

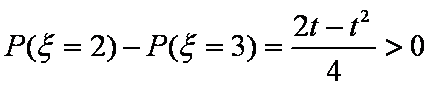
所以解得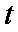
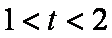
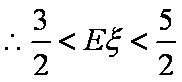
知识点
2013年12月21日上午10时,省会首次启动重污染天气Ⅱ级应急响应,正式实施机动车车尾号限行,当天某报社为了解公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
(1)完成被调查人员的频率分布直方图;
(2)若从年龄在[15,25),[25,35)的被调查者中各随机选取两人进行进行追踪调查,记选中的4人中不赞成“车辆限行”的人数为ξ,求随机变量ξ的分布列和数学期望。
正确答案
见解析
解析
(1)各组的频率分别是
所以图中各组的纵坐标分别是
……………………5分
(2)

所以
……11分
所以

知识点
扫码查看完整答案与解析