- 随机事件的关系
- 共394题








某城市环保局从该市市区


(1)从这

(2)从这



(3)根据这


正确答案
见解析
解析
(1)从茎叶图可知,空气质量为一级的有4天,为二级的有6天,超标的有5天
记“从

则
(2)




所以
…………………………………9分

(3)


所以估计一年中有
(说明:答243天,244天不扣分)
知识点
某超市在节日期间进行有奖促销,凡在该超市购物满300元的顾客,将获得一次摸奖机会,规则如下:
奖盒中放有除颜色外完全相同的1个红球,1个黄球,1个白球和1个黑球,顾客不放回的每次摸出1个球,若摸到黑球则停止摸奖,否则就要将奖盒中的球全部摸出才停止,规定摸到红球奖励10元,摸到白球或黄球奖励5元,摸到黑球不奖励。
(1)求1名顾客摸球3次停止摸奖的概率;
(2)记X为1名顾客摸奖获得的奖金数额,求随机变量X的分布列和数学期望。
正确答案
见解析
解析
(1)解:设“1名顾客摸球3次停止摸奖”为事件A,
则 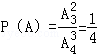
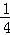
(2)解:随机变量X的所有取值为0,5,10,15,20.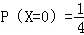
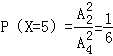
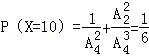
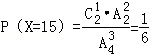
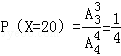
所以,随机变量X的分布列为:
知识点
某大楼共有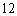
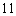
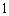
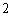
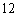
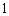
特殊原因,电梯只允许停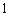
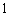
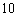
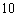
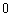
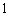
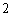
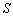
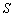
正确答案
解析
略
知识点
甲,乙,丙三位学生独立地解同一道题,甲做对的概率为





(1) 求至少有一位学生做对该题的概率;
(2) 求

(3) 求
正确答案
见解析。
解析

(1)由于事件“至少有一位学生做对该题”与事件“

(2)由题意知

整理得 

由


(3)由题意知



∴


知识点
在一次抽奖活动中,有甲、乙等6人获得抽奖的机会。抽奖规则如下:主办方先从6人中随机抽取两人均获奖1000元,再从余下的4人中随机抽取1人获奖600元,最后还从这4人中随机抽取1人获奖400元。
(1)求甲和乙都不获奖的概率;
(2)设X是甲获奖的金额,求X的分布列和均值
正确答案
见解析
解析
(1)设“甲和乙都不获奖”为事件A , ………………………………………1分
则P(A)=
答:甲和乙都不获奖的概率为
(2)X的所有可能的取值为0,400,600,1000,…………………………………………………6分
P(X=0)=


P(X=1000)=
∴X的分布列为
…………………………………11分
∴E(X)=0×



答: 甲获奖的金额的均值为500(元). ……………………………………………………………13分
知识点
扫码查看完整答案与解析