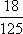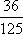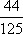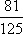- 随机事件的关系
- 共394题
市民李生居住在甲地,工作在乙地,他的小孩就读的小学在丙地,三地之间的道路情况如图所示.假设工作日不走其它道路,只在图示的道路中往返,每次在路口选择道路是随机的.同一条道路去程与回程是否堵车相互独立. 假设李生早上需要先开车送小孩去丙地小学,再返回经甲地赶去乙地上班.假设道路






(1)求李生小孩按时到校的概率;
(2)李生是否有七成把握能够按时上班?
(3)设

正确答案
见解析。
解析
(1)因为道路D、E上班时间往返出现拥堵的概率分别是

因此从甲到丙遇到拥堵的概率是
所以李生小孩能够按时到校的概率是
(2)甲到丙没有遇到拥堵的概率是
丙到甲没有遇到拥堵的概率也是
甲到乙遇到拥堵的概率是
甲到乙没有遇到拥堵的概率是

(3)依题意






分布列是:

知识点
方程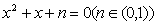
正确答案
解析
由一元二次方程有实根的条件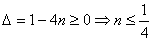
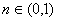
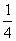
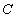
知识点
某产品经过4次革新后,成本由原来的120元下降到70元。若每次革新后,成本下降的百分率相同,那么,每次革新后成本下降的百分率为 (精确到0.1%)。
正确答案
12.6%
解析
略
知识点
盒子中装有形状、大小完全相同的3个红球和2个白球,从中随机取出一个记下颜色后放回,当红球取到2次时停止取球,那么取球次数恰为3次的概率是
正确答案
解析
略
知识点
在某校高三学生的数学校本课程选课过程中,规定每位同学只能选一个科目。已知某班第一小组与第二小组各有六位同学选择科目甲或科目乙,情况如下表:
现从第一小组、第二小组中各任选2人分析选课情况.
(1)求选出的4 人均选科目乙的概率;
(2) 设

正确答案
见解析。
解析
(1)设“从第一小组选出的2人选科目乙”为事件A,“从第二小组选出的2人选科目乙”为事件B,
由于事件A、B相互独立,且P(A)=

所以选出的4人均选科目乙的概率为:
P(A•B)=P(A)•P(B)=
(2)ξ可能的取值为0,1,2,3,
则P(ξ=0)=






ξ的分布列为:
所以ξ的数学期望为:0×



知识点
扫码查看完整答案与解析