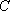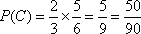- 随机事件的关系
- 共394题
一厂家向用户提供的一箱产品共10件,其中有1件次品. 用户先对产品进行随机抽检以决定是否接受. 抽检规则如下:至多抽检3次,每次抽检一件产品(抽检后不放回),只要检验到次品就停止继续抽检,并拒收这箱产品;若3次都没有检验到次品,则接受这箱产品,按上述规则,该用户抽检次数的数学期望是___________.
正确答案
解析
略
知识点
五个人站成一排照相,其中甲与乙不相邻,且甲与丙也不相邻的不同站法有
正确答案
解析
略
知识点
某车间在三天内,每天生产10件某产品,其中第一天,第二天分别生产出了1件、

正确答案

解析
(1)


(2)由第三项的二项式系数为

知识点
从1.2.3.4.5中任取2个不同的数,事件A=“取到的2个数之和为偶数”,事件B=“取到的2个数均为偶数”,则P(B|A)=( )
正确答案
解析
事件A=“取到的2个数之和为偶数”所包含的基本事件有:(1,3)、(1,5)、(3,5)、(2,4),
事件B=“取到的2个数均为偶数”所包含的基本事件有(2,4),
知识点
某班甲、乙两名同学参加l00米达标训练,在相同条件下两人10次训练的成绩(单位:秒)如下:
(1)请作出样本数据的茎叶图;如果从甲、乙两名同学中选一名参加学校的100米比赛,从成绩的稳定性方面考虑,选派谁参加比赛更好,并说明理由(不用计算,可通过统计图直接回答结论)。
(2)从甲、乙两人的10次训练成绩中各随机抽取一次,求抽取的成绩中至少有一个比12.8秒差的概率。
(3)经过对甲、乙两位同学的多次成绩的统计,甲、乙的成绩都均匀分布在[11.5,14.5]之间,现甲、乙比赛一次,求甲、乙成绩之差的绝对值小于0.8秒的概率。
正确答案
见解析。
解析
(1)茎叶图

从统计图中可以看出,乙的成绩较为集中,差异程度较小,应选派乙同学代表班级参加比赛更好;………………4分
(2)设事件A为:甲的成绩低于12.8,事件B为:乙的成绩低于12.8,
则甲、乙两人成绩至少有一个低于


(3)设甲同学的成绩为


得
如图阴影部分面积即为

知识点
某医药研究所开发一种新药,在实验药效时发现:如果成人按规定剂量服用,那么服药
后每毫升血液中的含药量



(1)试求药量峰值(


(2)如果每毫升血液中含药量不少于1微克时治疗疾病有效,那么成人按规定剂量服用该药一次后能维持多长的有效时间?(精确到0.01小时)
正确答案
(1)当
解析
解析:将

(1)当
∵
当
∵
∴
∴当
(2)∵


∴


当

当

∴当
∴有效的持续时间为:
知识点
李先生家住













(1)若走
(2)若走

(3)按照“平均遇到红灯次数最少”的要求,请你帮助李先生从上述两条路线中选择一条最好的上班路线,并说明理由。
正确答案
见解析。
解析
(1)设“走

则 
所以走

(2)依题意,



随机变量
所以
(3)设选择




因为

知识点
如图,矩形






正确答案
解析
略
知识点
某同学参加某高校自主招生3门课程的考试。假设该同学第一门课程取得优秀成绩的概率为



(1)求该生至少有1门课程取得优秀成绩的概率及求

(2)求数学期望
正确答案
见解析。
解析
解析:用


由题意得
(1)该生至少有一门课程取得优秀成绩的概率为
(2)
及
∴
∴该生取得优秀成绩的课程门数的期望为
知识点
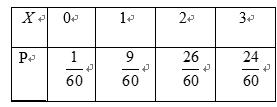
计算机考试分理论考试与实际操作考试两部分进行,每部分考试成绩只记“合格”与“不合格”,两部分考试都“合格”者,则计算机考试“合格”并颁发“合格证书”.甲、乙、丙三人在理论考试中“合格”的概率依次为:





(1)假设甲、乙、丙3人同时进行理论与实际操作两项考试,谁获得“合格证书”的可能性大;
(2)求这3人进行理论与实际操作两项考试后,恰有2人获得“合格证书”的概率;
(3)用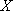
正确答案
见解析
解析
(1)记“甲获得合格证书”为事件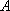
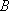
则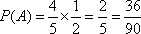
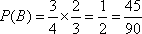
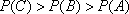
(2)设3人考试后恰有2人获得“合格证书”为事件
=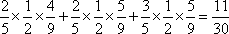
(3)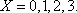
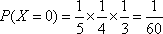
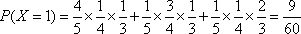
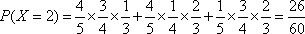
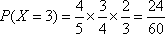
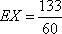
__________13分
知识点
扫码查看完整答案与解析