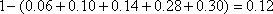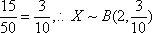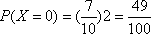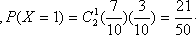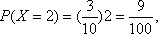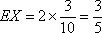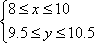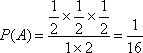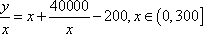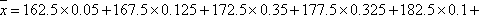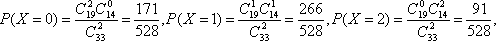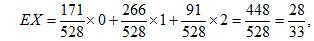- 随机事件的关系
- 共394题
有1位老师与2名女生2名男生站成一排合影,两名女生之间只有这位老师,这样的不同排法共有
正确答案
解析
略
知识点
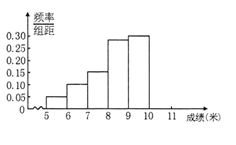
某市为了解今年高中毕业生的身体素质状况,从本市某校高中毕业班中抽取一个班进行实心球测试,成绩在8米及以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知第一小组为[5,6),从左到右前5个小组的频率分别为0.06,0.10,0.14,0.28,0.30.第 6 小组的频数是 6.
(1)求这次实心球测试成绩合格的人数;
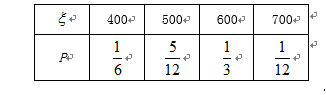
(2)用此次测试结果估计全市毕业生的情况.若从今年的高中毕业生中随机抽取两名,记X表示两人中成绩不合格的人数,求X的分布列及数学期望;
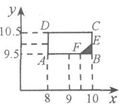
(3) 经过多次测试后,甲成绩在8〜10米之间,乙成绩在9.5〜10.5米之间,现甲、乙各投一次,求甲投得比乙远的概率。
正确答案
见解析。
解析
(1)第6小组的频率为
∴此次测试总人数为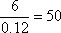
∴第4、5、6组成绩均合格,人数为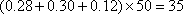
(2)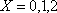
所求分布列为
(3)
设甲、乙各投掷一次的成绩分别为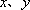
事件“甲投得比乙远的概率”满足的区域为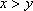
∴由几何概型
知识点
甲、乙两名同学在5次英语口语测试中的成绩统计如图5的茎叶图所示。
(1)现要从中选派一人参加英语口语竞赛,从两同学的平均成绩和方差分析,派谁参加更合适;
(2)若将频率视为概率,对学生甲在今后的三次英语口语竞赛成绩进行预测,记这三次成绩中高于



(注:样本数据




正确答案
见解析。
解析
(1)



因为

(2)甲高于80分的频率为



直接计算得



所以,
(或
知识点
目前,空气中的“PM2.5”(直径小于等于2.5微米的颗粒物)对人体健康的危害程度越来越受到人们的关注,世界卫生组织(WHO)在2005年就制定了“PM2.5”的准则值,某地区空气中“PM2.5”的浓度高于这个准则值,生活在该地区的居民死亡风险就会显著上升,WHO同时还设定了三个过渡期目标值,为目前还无法一步到位的地区提供阶段性目标(见下表,表中各数据均是相应标准的最高限值)。

(1)计算该市一年中“PM2.5”每日24小时平均浓度值分别达到(WHO)过渡期目标-1和
(WHO)准则值的天数;
(2)若将频率视为概率,记该市某一周空气中“PM2.5”日24小时平均浓度值达到(WHO)
准则值的天数为X,求X的数学期望;
(3)若将频率视为概率,求该市某一周至少有2天空气中“PM2.5”日24小时平均浓度值达到(WHO)准则值的概率,(结果精确到0.01)(参考数据:
正确答案
见解析。
解析
(1)该市一年中“PM2.5”日24小时平均浓度值达到世界卫生组织(WHO)过渡期-1的天数为:
一年中“PM2.5”日24小时平均浓度值达到(WHO)准则值的天数为:

(2)依题意知,该市一年中一天空气中“PM2.5”臼24小时平均浓度值达到(WHO)准则值的概率
因X服从二项分布,即

(3)因该市一年中一天空气中“PM2.5”日24小时平均浓度值达到(WHO)准则值的概率
则一天空气中“PM2.5”日24小时平均浓度值达不到(WHO)准则值的概率为:
故一周至少有2天空气中“PM2.5”日24小时平均浓度值达到(WHO)准则值的概率为:
知识点
某连锁超市有
(1)根据上面统计结果,求出
(2)已知每件该商品的销售利润为1元,
正确答案
见解析
解析
解:(1)B分店销售量为200件、300件、400件的频率分别为


(2)A分店销售量为200件、300件的频率均为
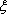
P(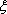
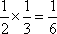
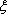
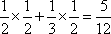
P(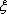
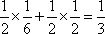
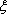
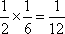
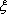
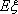

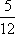

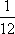
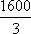
知识点
在我市“城乡清洁工程”建设活动中,社会各界掀起净化美化环境的热潮.某单位计划在小区内种植





(1)若出现


(2)求

(3)若出现恰好两棵树成活的的概率最大,试求
正确答案
见解析。
解析
(1)由题意,得

(2)
得
(3)由

∴
由上述不等式解得

知识点
有一个3×4×5的长方体, 它的六个面上均涂上颜色. 现将这个长方体锯成60个1×1×1的小正方体,从这些小正方体中随机地任取1个,设小正方体涂上颜色的面数为
(1)求

正确答案
见解析
解析
(1)60个1×1×1的小正方体中,没有涂上颜色的有6个,
(2)由(1)可知



分布列
E




知识点
某班从6名干部中(其中男生4人,女生2人)选3人参加学校的义务劳动。
(1)设所选3人中女生人数为


(2)求男生甲或女生乙被选中的概率;
(3)在男生甲被选中的情况下,求女生乙也被选中的概率。
正确答案
见解析。
解析
解析:(1)



(2)设“甲、乙都不被选中”为事件


(3)记“男生甲被选中”为事件




知识点
为保护环境,某单位采用新工艺,把二氧化碳转化为一种可利用的化工产品。已知该单位每月的处理量最多不超过300吨,月处理成本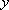

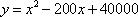
(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(2)要保证该单位每月不亏损,则每月处理量应控制在什么范围?
正确答案
见解析
解析
(1)由题意可知,二氧化碳的每吨平均处理成本为
……………………4分
因为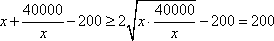
当且仅当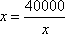
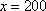
(2)设该单位每月获利为S(元),则
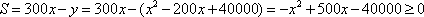
即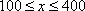
由题意可知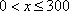
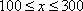
知识点
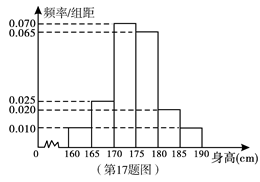
为了调查茂名市某中 学高三男学生的身高情况,在该中学高三男
学生中随机抽取了40名同学作为样本,测得他们的身高后,画出频率分布直方图如下:
(1)估计该校高三男学生的平均身高;
(2)从身高在170cm(含170cm)以上的样本中随机抽取2人,记身高在170~175cm之间的人数为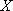
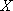
(部分参考数据: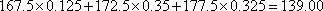
正确答案
见解析。
解析
(1)由频率分布直方图可知,该校高三男学生的平均身高为
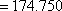
(2)由频率分布直方图可知,
所抽取的样本中身高在170~175cm之间的人数有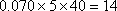
所抽取的样本中身高在170cm(含170cm)以上的人数有
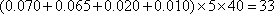
所以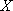
所以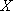
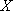
知识点
扫码查看完整答案与解析