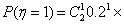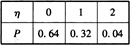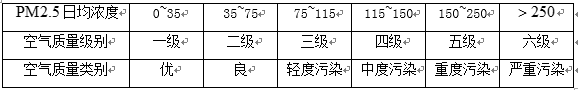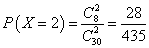- 随机事件的关系
- 共394题
设



(1)求方程
(2)求
正确答案
见解析。
解析
(1)
(2)

……1分

知识点
某学校的一间功能室统一使用某种节能灯管,已知这种灯管的使用寿命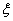
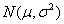
(1)求这种灯管的平均使用寿命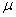
(2)假设一间功能室一次性换上2支这种新灯管,使用12个月时进行一次检查,将已经损坏的灯管换下(中途不更换),设需要更换的灯管数为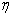
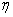
正确答案
见解析。
解析
(1)因为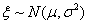
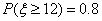
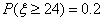
所以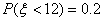
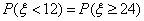
由正态分布密度曲线的对称性可知,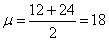
即这种灯管的平均使用寿命是18个月,(6分)
(2)这种灯管的使用寿命少于12个月的概率为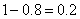
由题意知,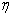
则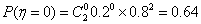
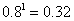
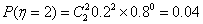
所以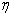
所以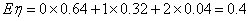
知识点
某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响. 已知某学生只选修甲的概率为0.08,只选修甲和乙的概率是0.12,至少选修一门的概率是0.88,用
(1)记“函数
(2)求的
正确答案
见解析。
解析
解析:(1)设该学生选修甲、乙、丙的概率分别为

依题意得
若函数

当


(2)依题意知
则
∴

知识点
深圳市某校中学生篮球队假期集训,集训前共有6个篮球,其中3个是新球(即没有用过的球),3个是旧球(即至少用过一次的球),每次训练,都从中任意取出2个球,用完后放回。
(1)设第一次训练时取到的新球个数为

(2)求第二次训练时恰好取到一个新球的概率。
正确答案
见解析。
解析
(1)
设“第一次训练时取到










(2)设“从6个球中任意取出2个球,恰好取到一个新球”为事件
则“第二次训练时恰好取到一个新球”就是事件
而事件


所以,
由条件概率公式,得



所以,第二次训练时恰好取到一个新球的概率为

知识点
某市地铁连同站台等附属设施全部建成后,平均每1公里需投资人民币1亿元.全部投资都从银行贷款.从投入营运那一年开始,地铁公司每年需归还银行相同数额的贷款本金0.05亿元.这笔贷款本金先用地铁营运收入支付,不足部分由市政府从公用经费中补足. 地铁投入营运后,平均每公里年营运收入(扣除日常管理费等支出后)第一年为0.0124亿元,以后每年增长20%,到第20年后不再增长.求:
(1)地铁营运几年,当年营运收入开始超过当年归还银行贷款本金?
(2)截至当年营运收入超过当年归还银行贷款本金的那一年,市政府已累计为1公里地铁支付多少元费用?(精确到元,1亿=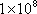
正确答案
见解析
解析
(1)地铁营运第
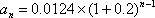
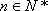
根据题意有: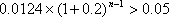
解得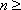
(或者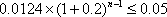
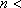
答:地铁营运9年,当年营运收入开始超过当年归还银行贷款本金. …………6分
(2)市政府各年为1公里地铁支付费用
第1年: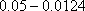
第2年: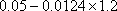
第
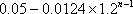

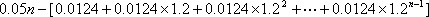
将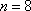
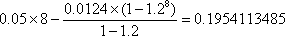
答:截至当年营运收入超过当年归还银行贷款本金的那一年,市政府累计为一公里地铁共支付19541135元费用. ………………………………………………9分
知识点
空气质量指数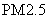
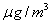
某市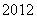
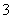
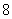
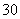
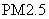
(1)估计该城市一个月内空气质量类别为良的概率;
(2)在上述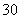
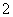
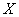
质量类别为优的天数,求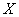
正确答案
见解析。
解析
(1)由条形统计图可知,空气质量类别为良的天数为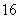
所以此次监测结果中空气质量类别为良的概率为 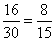
(2)随机变量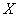
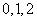
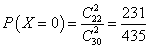
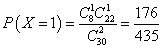
所以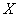
知识点
随机调查某社区

(1)将此样本的频率估计为总体的概率,随机调查



(2)根据以上数据,能否有

参考公式:

参考数据:
正确答案
见解析。
解析
(1)依题意,随机变量

方法一:





方法二:根据题意可得



(2)提出假设
根据样本提供的

因为当



知识点
甲、乙两人参加某电视台举办的答题闯关游戏,按照规则,甲先从6道备选题中一次性抽取3道题独立作答,然后由乙回答剩余3题,每人答对其中2题就停止答题,即闯关成功,已知在6道备选题中,甲能答对其中的4道题,乙答对每道题的概率都是
(1)求甲、乙至少有一人闯关成功的概率;
(2)设甲答对题目的个数为

正确答案
见解析。
解析
(1)设甲、乙闯关成功分别为事件A、B,
则

事件
则甲、乙至少有一人闯关成功的概率是

(2)由题知


则
所以
知识点
为迎接2013年“两会”(全国人大3月5日-3月18日、全国政协3月3日-3月14日)的胜利召开,某机构举办猜奖活动,参与者需先后回答两道选择题,问题A有四个选项,问题B有五个选项,但都只有一个选项是正确的,正确回答问题A可获奖金

正确答案
见解析。
解析
该参与者随机猜对问题A的概率
随机猜对问题B的概率
回答问题的顺序有两种,分别讨论如下:
①先回答问题A,再回答问题B,参与者获奖金额

则


数学期望
②先回答问题B,再回答问题A,参与者获奖金额

则


数学期望

于是,当

当

当

知识点
某学生参加某高校的自主招生考试,须依次参加A、B、C、D、E五项考试,如果前四
项中有两项不合格或第五项不合格,则该考生就被淘汰,考试即结束;考生未被淘汰时,一定继续参加后面的考试。已知每一项测试都是相互独立的,该生参加A、B、C、D四项考试不合格的概率均为
(1)求该生被录取的概率;
(2)记该生参加考试的项数为

正确答案
见解析。
解析
(1)若该生被录取,则前四项最多有一项不合格,并且第五项必须合格
记A={前四项均合格}
B={前四项中仅有一项不合格}
则P(A)=
P(B)=
又A、B互斥,故所求概率为
P=P(A)+P(B)=
(2)该生参加考试的项数



……………………………………10分

知识点
扫码查看完整答案与解析