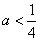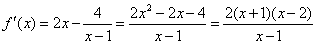- 简单复合函数的导数
- 共526题
1
题型:
单选题
|
已知向量


则
正确答案
A
解析
略
知识点
简单复合函数的导数
1
题型:简答题
|
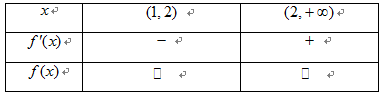
已知函数
(1)讨论函数
(2)若函数


正确答案
(1)
解析
(1)
若


即








若


即







∴当





(2)因函数



即
由


由于当
∴
知识点
简单复合函数的导数
1
题型:
单选题
|
设






正确答案
D
解析
略
知识点
简单复合函数的导数
1
题型:简答题
|
已知函数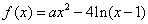
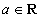
(1)当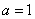
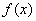
(2)已知点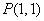
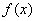
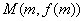
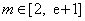
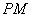
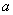
正确答案
(1)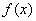
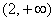
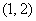
(2)
解析
(1)当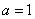
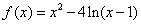
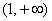
所以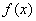
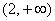
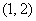
(2)因为对任意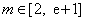
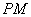
所以对任意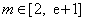
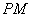
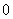
即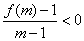
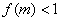
即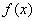
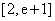
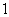
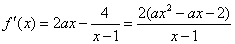
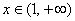
令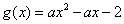
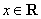
(1)当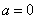
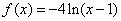
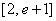
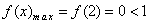
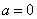
(2)当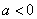
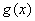
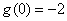
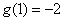
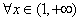
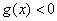
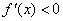

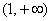
故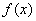
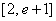
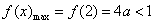
所以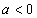
(3)当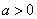
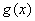
且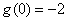
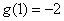
所以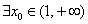
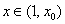
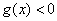
当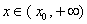
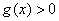
所以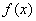
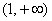
故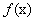
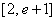
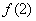
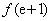
所以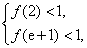
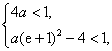
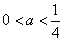
综上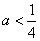
知识点
简单复合函数的导数
1
题型:填空题
|
若B且a1+a2=28,则在展开式的各项系数中,最大值等于 。
正确答案
35
解析
略
知识点
简单复合函数的导数
下一知识点 : 定积分
扫码查看完整答案与解析