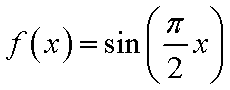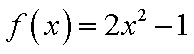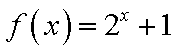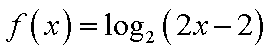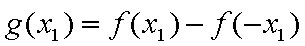- 利用导数证明不等式
- 共265题
在






正确答案
解析
略
知识点
已知集合



正确答案
解析
由所定义的运算可知


知识点
执行如图所示的程序框图,若输入的x的值为3,则输出的n的值为______.
正确答案
解析
略
知识点
对于函数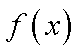
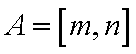
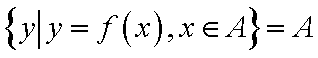
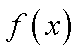
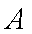
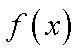
正确答案
解析
略
知识点
已知平面上的点集













正确答案
答案:2;
解析
略
知识点
已知

(1)求函数
(2)求证:当


正确答案
见解析
解析
解析:(1)


∴当


(2)当


当


设

∵




当



因此当


知识点
已知函数f(x)=(3x2-6X+6)ex-x3
(1)求函数f(x)的单调区间及极值;
(2)若 x1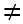
正确答案
见解析。
解析
(1)∵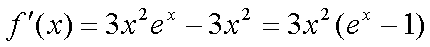
∴当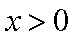
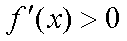
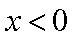
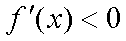
则
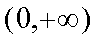
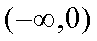
所以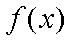
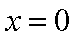
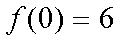
(2)∵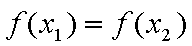
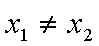
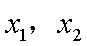
不妨设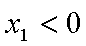

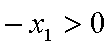
令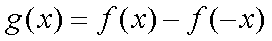
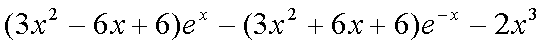
则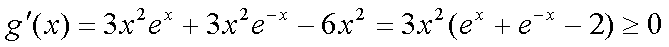
所以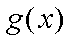
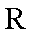
又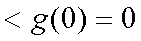
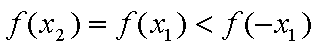
又∵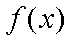
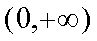
∴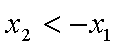

知识点
设函数
(1)当

(2)若函数

正确答案
(1){x|

(2)
解析
(1)当










(2)由题可知





知识点
已知点







正确答案
解析






知识点
设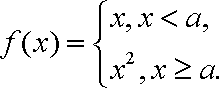

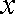
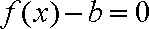
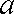
正确答案
答案:
解析
略
知识点
扫码查看完整答案与解析