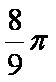- 利用导数证明不等式
- 共265题
等差数列





正确答案

解析
由







知识点
已知函数

(1)若曲线




(2)在(1)的条件下,证明


(3)若




正确答案
见解析。
解析
(1)

∵曲线


∴ 

(2)设
则
∴当





在
∴


∴

(3)原方程可化为
令



















又



知识点
如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D、E分别在棱PB、PC上,且DE∥BC。
(1)求证:BC⊥平面PAC;
(2)当D为PB的中点时,求AD与平面PAC所成的角的正弦值;
(3)是否存在点E使得二面角A-DE-P为直二面角?并说明理由。
正确答案
见解析
解析
(1)∵PA⊥底面ABC,∴PA⊥BC。
又∠BCA=90°,∴AC⊥BC,∴BC⊥平面PAC。
(2)∵D为PB的中点,DE∥BC,
∴DE=
又由(1)知,BC⊥平面PAC,
∴DE⊥平面PAC,垂足为点E,
∴∠DAE是AD与平面PAC所成的角。
∵PA⊥底面ABC,∴PA⊥AB。
又PA=AB,∴△ABP为等腰直角三角形,
∴AD=
在Rt△ABC中,∠ABC=60°,∴BC=
∴在Rt△ADE中,sin∠DAE=
即AD与平面PAC所成角的正弦值为
(3)∵DE∥BC,又由(1)知,BC⊥平面PAC,
∴DE⊥平面PAC。
又∵AE

∴DE⊥AE,DE⊥PE,
∴∠AEP为二面角A-DE-P的平面角。
∵PA⊥底面ABC,∴PA⊥AC,
∴∠PAC=90°,∴在棱PC上存在一点E,使得AE⊥PC。
这时,∠AEP=90°,
故存在点E使得二面角A-DE-P是直二面角。
知识点
若复数z满足:(3﹣i)z=3+i(i为虚数单位),则复数z在复平面内对应的点所在的象限是( )
正确答案
解析


知识点
已知



(1)求函数
(2)若




正确答案
见解析
解析
(1)




单调增区间为
(2)由余弦定理得,

知识点
过点P(1 ,4)作直线L交 x轴、y轴正半轴于A、B两点,O为坐标原点,当OA+OB取最小值时,求直线L方程.
正确答案
见解析
解析
解法1:设直线的斜率为k,因为直线与x轴y轴正半轴分别相交,所以k<0
因为经过点P(1,4),
则直线I的方程为I:y-4=k(x-1)
整理得:kx-y+4-k=0
当x=0时,y=|OB|=4-k>0
当y=0时,x=|OA|=(k-4)/k>0
|OA|+|OB|=(4-k)+(k-4)/k=4-k+1-4/k=(-k)+(-4/k)+5
由于-k>0,-4/k>0,故-k+(-4/k)>=2根号(-k*(-4/k))=4.
那么最小值=5+4=9
当-k=-4/k,即k=-2,取"=".
直线L方程:y=2x+2
解法2:设A(a,0),B(0,b),a>0,b>0
则:AB直线方程为: x/a+y/b=1
所以,1/a+4/b=1
所以,a=b/(b-4)=1+4/(b-4)
a+b=[1+4/(b-4)]+[(b-4)+4]
=5+[4/(b-4)+(b-4)]
≥5+2√4
=9
其中,4/(b-4)=(b-4),即:b=6时,a+b最小
b=6时,a=1+4/(b-4)=3
所以,OA+OB取最小值时,直线L方程为:x/3+y/6=1.
知识点
某高校组织自主招生考试,共有2 000名优秀同学参加笔试,成绩均介于195分到275分之间,从中随机抽取50名同学的成绩进行统计,将统计结果按如下方式分成8组:第1组[195,205),第2组[205,215),…,第8组[265,275],如图是按上述分组方法得到的频率分布直方图,且笔试成绩在260分(含260分)以上的同学进入面试。
(1)估计所有参加笔试的2 000名同学中,参加面试的同学人数;
(2)面试时,每位同学抽取两个问题,若两个问题全答错,则不能取得该校的自主招生资格;若两个问题均回答正确且笔试成绩在270分以上,则获A类资格;其他情况下获B类资格,现已知某中学有两人获得面试资格,且仅有一人笔试成绩为270分以上,在回答两个面试问题时,两人对每一个问题正确回答的概率均为,求恰有一名同学获得该高校B类资格的概率。
正确答案
见解析
解析
(1)设第i(i=1,2,…,8)组的频率为fi,则由频率分布直方图知
f7=1-(0.004+0.01+0.01+0.02+0.02+0.016+0.008)×10=0.12.
所以成绩在260分以上的同学的概率P≈+f8=0.14,
∴2 000×0.14=280,
故这2 000名同学中,取得面试资格的约为280 …… 6分
(2)不妨设两名同学分别为M,N,且M的笔试成绩在270分以上,则对于M,答题的可能有M11,M10,M01,M00,对于N,答题的可能有N11,N10,N01,N00,
其中角标中的1表示正确,0表示错误,如N10表示N同学第一题正确,第二题错误。
将两名同学的答题情况列表如下:
表中AB表示M获A类资格,N获B类资格;
BC表示M获B类资格,N没有获得资格。
所以恰有一名同学获得该高校B类资格的概率为=. …… 12分
知识点
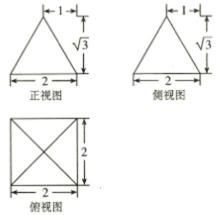
某几何体的三视图如图所示,这个几何体的内切球的体积为
正确答案
解析
此几何体是底面边长为2,高为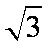
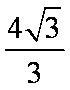
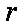
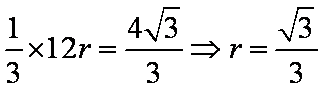
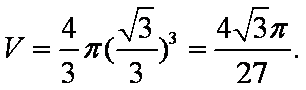
知识点
某校高三年级在高校自主招生期间,把学生的平时成绩按“百分制”折算并排序,选出前300名学生,并对这300名学生按成绩分组,第一组[75,80),第二组[80,85),第三组[85,90),第四组[90,95),第五组[95,100),其中第五组、第一组、第四组、第二组、第三组、的人数依次成等差数列,如图为频率分布直方图的一部分
(1) 请在图中补全频率分布直方图
(2) 若B大学决定在成绩高的第4,5组中用分层抽样的方法抽取6名学生,并且分成2组,每组3人进行面试,求95分(包括95分)以上的同学在同一个小组的概率。
正确答案
见解析。
解析
(1)由图象可知第五组为:0.02×5×300=30人,由题意,第五组,第一组,第四组,第二组,第三组的人数依次是30人,45人,60人,75人,90人。
(2)第四组中抽取人数:

知识点
执行如图所示的程序框图后,输出的值为4,则P的取值范围是( )
正确答案
解析
执行程序框图依次得

知识点
扫码查看完整答案与解析