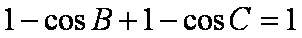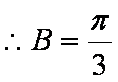利用导数证明不等式
共265题

· 利用导数证明不等式

利用导数证明不等式
共265题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

某几何体的三视图如图所示，则它的表面积为( )

正确答案

解析

略

知识点

利用导数证明不等式

题型：单选题

单选题 · 5 分

如图，平面内有三个向量，其中与的夹角为，与的夹角为，且，若，则

正确答案

解析

设与同方向的单位向量分别为，依题意有，又，，则，所以. 故选C.

知识点

利用导数证明不等式

题型：填空题

填空题 · 5 分

如图，测量河对岸的塔高时，可以选与塔底在同一水平面内的两个观测点与，测得，，米，并在测得塔顶的仰角为，则塔的高度

正确答案

解析

在中，根据正弦定理得，

在中，为所求.

知识点

利用导数证明不等式

题型：单选题

单选题 · 5 分

2014年3月，为了调查教师对第十二届全国人民代表大会二次会议的了解程度，安庆市拟采用分层抽样的方法从三所不同的中学抽取60名教师进行调查.已知学校中分别有180，270，90名教师，则从学校中应抽取的人数为（）.

A10

B12

C18

D24

正确答案

解析

从学校中应抽取的人数为,选A.

知识点

利用导数证明不等式

题型：简答题

简答题 · 10 分

设函数。

（1）求不等式的解集；

（2），使，求实数的取值范围。

正确答案

见解析

解析

解析：

（1），…………2分

当

综上所述 ………………5分

（2）易得，若都有恒成立，

则只需解得………………10分

知识点

利用导数证明不等式

题型：填空题

填空题 · 5 分

将函数y=3sin2x的图象向左平移个单位后所得到的函数图象对应的解析式为　　。

正确答案

y=3sin（2x+）

解析

将函数y=3sin2x的图象向左平移个单位后所得到的函数图象对应的解析式为：y=3sin[2（x+）]=3sin（2x+）。

知识点

利用导数证明不等式

题型：简答题

简答题 · 10 分

设函数，。

（1）解不等式；

（2）设函数，且在上恒成立，求实数的取值范围。

正确答案

（1）

（2）[-4,0]

解析

（1）由条件知，

由，解得. (5分)

（2）由得，由函数的图像可知的取值范围是. (10分)

知识点

利用导数证明不等式

题型：简答题

简答题 · 12 分

在中，，，分别是三内角A，B，C所对的三边，已知。

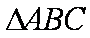
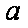
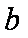
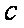
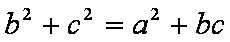
（1）求角A的大小；

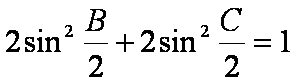
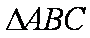
（2）若，试判断的形状。

正确答案

见解析

解析

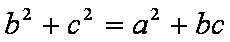
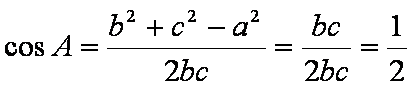
解析：（1），所以，又

得到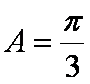…………4分

（2）∵ ∵

∴，…………6分

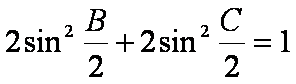
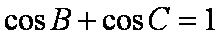
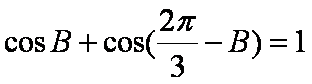
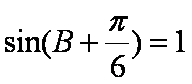
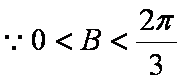
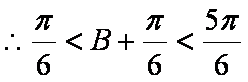
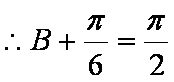
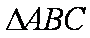
即，得到，…………8分

为等边三角形…………12分

知识点

利用导数证明不等式

题型：简答题

简答题 · 10 分

在极坐标系内，已知曲线的方程为，以极点为原点，极轴方向为正半轴方向，利用相同单位长度建立平面直角坐标系，曲线的参数方程为（为参数）。

（1）求曲线的直角坐标方程以及曲线的普通方程；

（2）设点为曲线上的动点，过点作曲线的两条切线，求这两条切线所成角余弦值的取值范围。

正确答案

（1）C1：(x-1)2+(y+2)2=1；C2：3x+4y-15=0

（2）

解析

（1）对于曲线的方程为，

可化为直角坐标方程，即；

对于曲线的参数方程为（为参数），

可化为普通方程. (5分)

（2）过圆心点作直线的垂线，此时两切线成角最大，即余弦值最小. 则由点到直线的距离公式可知，，则，因此，

因此两条切线所成角的余弦值的取值范围是. (10分)

知识点

利用导数证明不等式

题型：单选题

单选题 · 5 分

已知f（x）是偶函数，当，x∈[0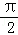，]时，f（x）=xsinx，若a=f（cos1），b=f（cos2），c=f（cos3），则 a，b，c 的大小关系为（　　）

Aa＜b＜c

Bb＜a＜c

Cc＜b＜a

Db＜c＜a

正确答案

解析

由于已知f（x）是偶函数，∴f（﹣x）=f（x），再由f（x）=xsinx，可得函数f（x）在[0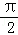，]上是增函数。

再由a=f（cos1），b=f（cos2）=f（﹣cos（π﹣2））=f（cos（π﹣2），c=f（cos3）=f（﹣cos（π﹣3））=f（cos（π﹣3），

而且 cos（π﹣3）＞cos1＞cos（π﹣2），故有c＞a＞b，

故选B。

知识点

利用导数证明不等式

继续学习学习下一知识点

下一知识点 : 利用导数求参数的取值范围

百度题库 > 高考 > 文科数学 > 利用导数证明不等式

扫码查看完整答案与解析