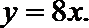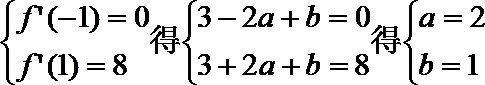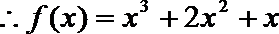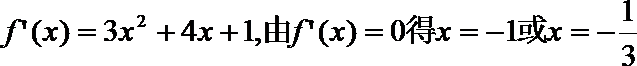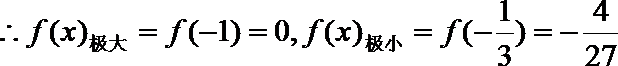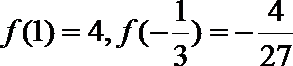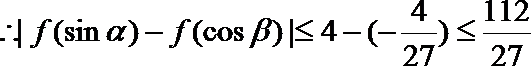利用导数证明不等式
共265题

· 利用导数证明不等式

利用导数证明不等式
共265题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

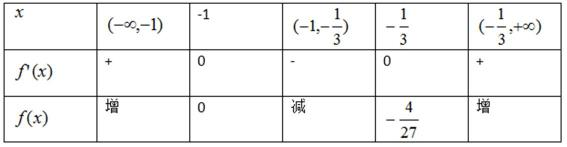
21．已知函数为常数，e=2.71828…是自然对数的底数)，曲线在点处的切线与x轴平行.

（1）求的单调区间；

（2）设，其中为的导函数.证明：对任意.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的几何意义利用导数研究函数的单调性利用导数证明不等式

题型：简答题

简答题 · 12 分

22．函数处取得极值，且的图象在处

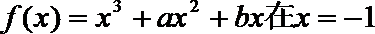
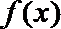
的切线平行于直线

（I）求函数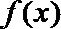解要式和极值；

（II）对任意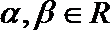，求证。

正确答案

解：（I）由

则

（II）

由（I）知上的最大，最小值分别为

解析

解析已在路上飞奔，马上就到！

知识点

导数的几何意义利用导数研究函数的单调性利用导数求函数的极值利用导数证明不等式

题型：单选题

单选题 · 5 分

9. 已知一个空间几何体的三视图如图所示，

根据图中标出的尺寸（单位：cm），可得这个

几何体的体积是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用导数证明不等式

题型：单选题

单选题 · 5 分

11.已知函数的图像如图所示，则函数的图像可能是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用导数证明不等式

题型：简答题

简答题 · 13 分

21．已知函数。

（1）求函数的单调区间；

（2）若函数的图像在点处的切线的倾斜角为，对于任意的，函数在区间上总不是单调函数，求的取值范围；

（3）求证：。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的几何意义利用导数研究函数的单调性利用导数证明不等式利用导数求参数的取值范围

题型：简答题

简答题 · 13 分

21.已知偶函数满足：当

（Ⅰ）求表达式；

（Ⅱ）若直线与函数的图像恰有两个公共点，求实数的取值范围；

（Ⅲ）试讨论当实数满足什么条件时，直线的图像恰有个公共点，且这个公共点均匀分布在直线上。（不要求过程）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用导数证明不等式

题型：简答题

简答题 · 14 分

20．已知函数，且在时函数取得极值.

（Ⅰ）求的值及的极值；

（Ⅱ）若，证明：当时，的图象恒在的上方.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用导数求函数的极值利用导数求函数的最值利用导数证明不等式

题型：简答题

简答题 · 14 分

21．已知函数

（1）求的单调区间；

（2）时，判断方程:根的个数并说明理由；

（3）有两个极值点且证明:.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用导数研究函数的单调性利用导数求函数的极值利用导数证明不等式

题型：单选题

单选题 · 5 分

8．连接球面上两点的线段称为球的弦，半径为4的球的两条弦AB、CD的长度分别为2和4，M，N分别是AB、CD的中点，两条弦的两端都在球面上运动，有下面四个命题：

①弦AB、CD可能相交于点M；

②弦AB、CD可能相交于点N；

③MN的最大值是5；

④MN的最大值是1.

其中所有正确命题的序号为（）

A①③④

B①②③

C①②④

D②③④

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用导数证明不等式

题型：单选题

单选题 · 5 分

3. 某几何体的三视图如图所示，则它的表面积为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用导数证明不等式

继续学习学习下一知识点

下一知识点 : 利用导数求参数的取值范围

百度题库 > 高考 > 文科数学 > 利用导数证明不等式

扫码查看完整答案与解析