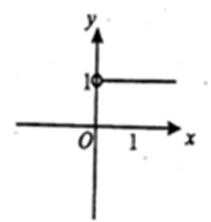
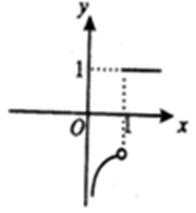
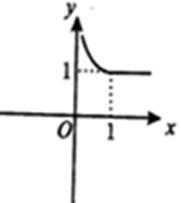
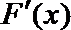利用导数证明不等式
共265题

· 利用导数证明不等式

利用导数证明不等式
共265题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 14 分

21．已知函数

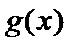
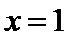
（Ⅰ）求在处的切线方程；

（Ⅱ）求的单调区间；

（Ⅲ）若，求证：．

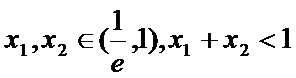
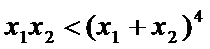
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的几何意义利用导数研究函数的单调性利用导数证明不等式

题型：简答题

简答题 · 14 分

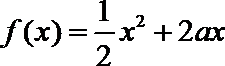
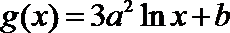
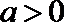
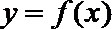
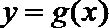
22．已知定义在正实数集上的函数，，其中．设两曲线，有公共点，且在该点处的切线相同。

（I）用表示，并求的最大值；

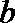
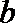
（II）求证：（）。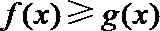

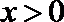
正确答案

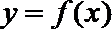
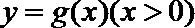
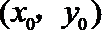
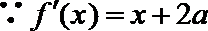
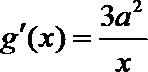
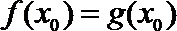
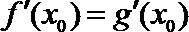
（Ⅰ）设与在公共点处的切线相同。

，，由题意，．

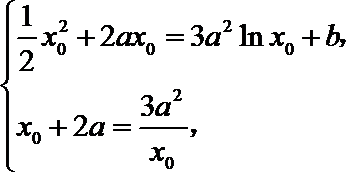
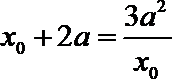
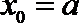
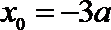
即由得：，或（舍去）。

即有．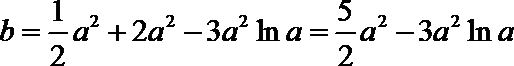

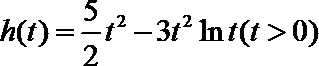
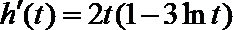
令，则．于是

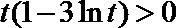
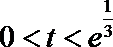
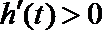
当，即时，；

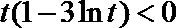
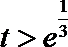
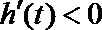
当，即时，．

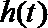
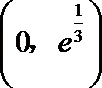
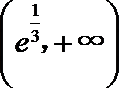
故在为增函数，在为减函数，

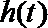
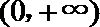
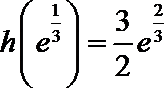
于是在的最大值为．

（Ⅱ）设，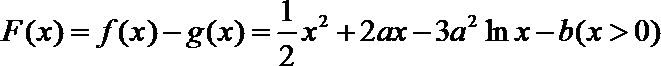

则．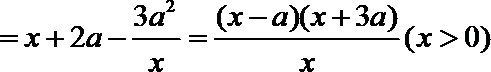

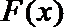
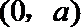
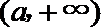
故在为减函数，在为增函数，

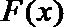
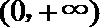
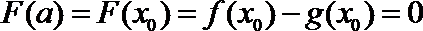
于是函数在上的最小值是．

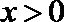
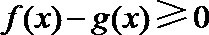
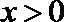
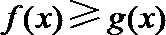
故当时，有，即当时，．

解析

解析已在路上飞奔，马上就到！

知识点

导数的几何意义利用导数研究函数的单调性利用导数求函数的最值利用导数证明不等式

题型：单选题

单选题 · 5 分

7．函数的图象大致是（）

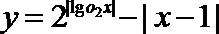
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用导数证明不等式

题型：填空题

填空题 · 4 分

7．若函数y=sin2x+acos2x的图象关于直线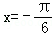对称，则a=　_________　．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用导数证明不等式

题型：简答题

简答题 · 14 分

20．在△ABC中，角A，B，C的对边分别为，

（1）求sinC的值；

（2）求△ABC的面积

正确答案

解：（1）∵A、B、C为△ABC的内角，

且＞0，所以A为锐角，

则sinA==

∴

∴；

（2）由（1）知，

又∵，

∴在△ABC中，由正弦定理，得

∴．

∴△ABC的面积．

解析

解析已在路上飞奔，马上就到！

知识点

利用导数证明不等式

题型：简答题

简答题 · 14 分

21．已知函数。

（1）实数为何值时，使得在内单调递增；

（2）证明：

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用导数研究函数的单调性利用导数求函数的最值利用导数证明不等式

题型：填空题

填空题 · 4 分

15．直线与圆交于两点，若，则实数=__________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用导数证明不等式

题型：单选题

单选题 · 5 分

1．已知，i是虚数单位，若，则的值等于（）

A-6

B-2

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用导数证明不等式

题型：简答题

简答题 · 14 分

21．已知点P（4，4），圆C：与椭圆E：有一个公共点A（3，1），F1、F2分别是椭圆的左、右焦点，直线PF1与圆C相切．

（1）求m的值与椭圆E的方程；

（2）设Q为椭圆E上的一个动点，求的取值范围．

正确答案

（1）点A代入圆C方程，

得．

∵m＜3，∴m＝1

圆C：．

设直线PF1的斜率为k，

则直线PF1的方程为：，

即．

∵直线PF1与圆C相切，

∴．

解得．

当k＝时，直线PF1与x轴的交点F1的横坐标为，不合题意，舍去．

当k＝时，直线PF1与x轴的交点F1的横坐标为－4，

∴c＝4．，

2a＝|AF1|＋|AF2|＝，，

a2＝18，b2＝2．

椭圆E的方程为：

（2），设Q（x，y），

，．

∵，即，

而，

∴－18≤6xy≤18

所以，的取值范围是[0，36]

的取值范围是[－6，6]．

∴的取值范围是[－12，0]

解析

解析已在路上飞奔，马上就到！

知识点

利用导数证明不等式

题型：单选题

单选题 · 5 分

5.双曲线的渐近线方程是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用导数证明不等式

继续学习学习下一知识点

下一知识点 : 利用导数求参数的取值范围

百度题库 > 高考 > 文科数学 > 利用导数证明不等式

扫码查看完整答案与解析