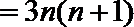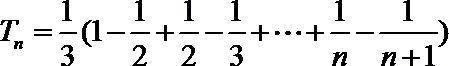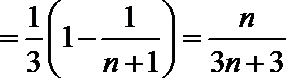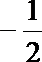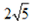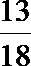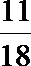- 利用导数证明不等式
- 共265题
21．在平面直角坐标
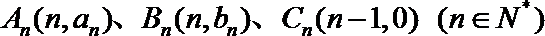
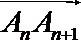
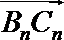
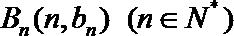
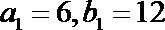
（1）数列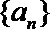
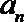
（2）数列{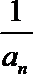
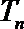
正确答案
（1）∵点Bn(n,bn)(n∈N*)都在斜率为6的同一条直线上，
∴
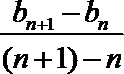
即bn+1-bn=6,
于是数列{bn}是等差数列，故bn=12+6(n-1) =6n+6.
∵
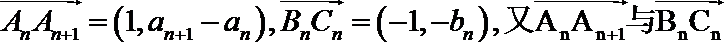
∴1×(-bn)－(-1)(an+1-an )=0,即an+1-an=bn
∴当n≥2时，an=a1+(a2-a1)+(a3-a2)+ …+(an-an-1)=a1+b1+b2+b3+…+bn-1
=a1+b1(n-1)+3(n-1)(n-2)
当n=1时，上式也成立。
所以an=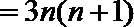
（2） 
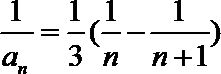
解析
解析已在路上飞奔，马上就到！
知识点
1．复数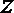
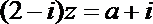
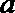
A
B2
C- 2
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
13．已知抛物线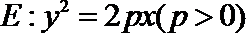
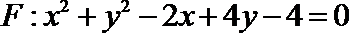
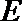
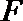
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11．已知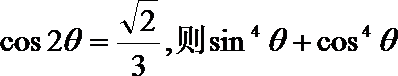
A
B
C
D－1
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
21．已知数列
（1）证明：数列
（2）设
正确答案
证明：（1)由
当
即
∴
又
∴
∴
解析
解析已在路上飞奔，马上就到！
知识点
11．如图1所示，正△ABC中，CD是AB边上的高，E、F分别是AC、BC的中点．现将△ACD沿CD折起，使平面
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8．已知双曲线
A
B2
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
15．P是以F1，F2为焦点的椭圆
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9．函数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
扫码查看完整答案与解析