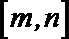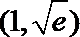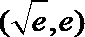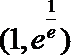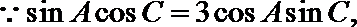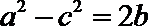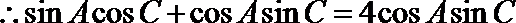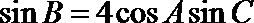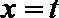- 利用导数证明不等式
- 共265题
1
题型:
单选题
|
15.设集合



正确答案
B
解析
解析已在路上飞奔,马上就到!
知识点
利用导数证明不等式
1
题型:
单选题
|
12.对于函数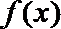
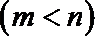
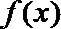
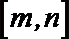
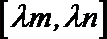
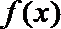
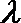
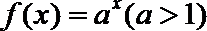
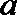
正确答案
C
解析
解析已在路上飞奔,马上就到!
知识点
利用导数证明不等式
1
题型:简答题
|
20.在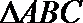
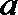
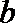
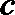
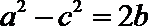
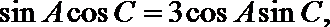
正确答案
解法一:在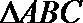
则由正弦定理及余弦定理有:
a·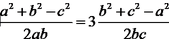
化简并整理得: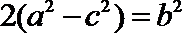
又由已知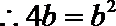
解得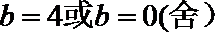

解法二:由余弦定理得:
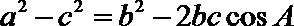
又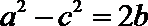
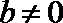
所以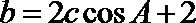
又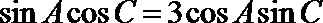
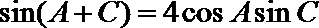
即
由正弦定理得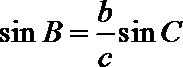
故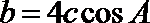
由①,②解得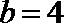
解析
解析已在路上飞奔,马上就到!
知识点
利用导数证明不等式
1
题型:
单选题
|
12.对于任意实数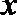
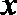
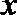
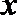
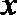
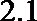
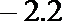
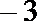
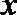
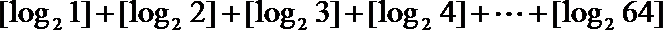
正确答案
C
解析
解析已在路上飞奔,马上就到!
知识点
利用导数证明不等式
1
题型:填空题
|
13.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
利用导数证明不等式
1
题型:简答题
|
21.已知函数

(1)当

(2)求函数
(3)当






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
利用导数研究函数的单调性利用导数求函数的极值利用导数求函数的最值利用导数证明不等式
1
题型:简答题
|
20. 设函数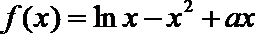
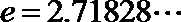
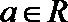
(Ⅰ)当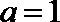
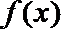
(Ⅱ)若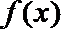
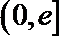
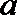
(Ⅲ)设函数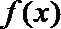
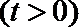
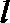
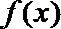
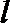
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
导数的几何意义利用导数研究函数的单调性利用导数求函数的极值利用导数证明不等式利用导数求参数的取值范围
1
题型:简答题
|
19. 已知数列


(1)当

(2)若




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
利用导数证明不等式
1
题型:
单选题
|
1.设函数
正确答案
D
解析
解析已在路上飞奔,马上就到!
知识点
利用导数证明不等式
1
题型:
单选题
|
8.下列函数中,以
正确答案
B
解析
解析已在路上飞奔,马上就到!
知识点
利用导数证明不等式
下一知识点 : 利用导数求参数的取值范围
扫码查看完整答案与解析