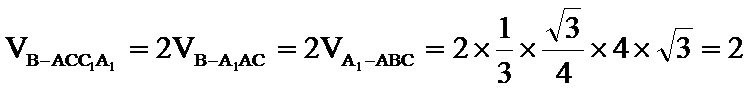利用导数证明不等式
共265题

· 利用导数证明不等式

利用导数证明不等式
共265题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

16．已知向量，函数，且图象上一个最高点的坐标为，与之相邻的一个最低点的坐标为.

（1）求的解析式；

（2）在△ABC中，是角A、B、C所对的边，且满足，求角B的大小以及的取值范围.

正确答案

解：（1） .

图象上一个最高点的坐标为，与之相邻的一个最低点的坐标为.

，

于是. 所以.

（2），

又，.

.于是，

. 所以.

解析

解析已在路上飞奔，马上就到！

知识点

利用导数证明不等式

题型：填空题

填空题 · 5 分

14．设函数___________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用导数证明不等式

题型：简答题

简答题 · 12 分

21．函数在上是增函数，在上是减函数．

（Ⅰ）求的取值范围；

（Ⅱ）解关于的不等式.

正确答案

解：

（Ⅰ）

由函数在上是增函数，在上是减函数

∴是的极大值

∴的两根为

∴

（Ⅱ）

∵对应方程的根为

∵ ∴

∴解集为

解析

解析已在路上飞奔，马上就到！

知识点

利用导数研究函数的单调性利用导数证明不等式利用导数求参数的取值范围

题型：单选题

单选题 · 5 分

8．已知各项为正的等比数列中，与的等比中项为，则的最小值为（）

A16

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用导数证明不等式

题型：简答题

简答题 · 12 分

20．已知函数f（x）=（e是自然对数的底数，其中常数a，b满足a＞b，且a+b=1，函数y=f（x）的图象在点（1，f（1））处的切线斜率是2﹣．

（Ⅰ）求a，b的值；

（Ⅱ）求函数f（x）的单调区间。

正确答案

解：（Ⅰ）f（x）=的导数为f′（x）=（x＞0），

由f′（1）=2﹣，得=2﹣，由a+b=1，可得=2﹣，

即=，由a＞b，a，则a=e，b=1﹣e；

（Ⅱ）由（Ⅰ）可得f′（x）=（x＞0），

即f′（x）=（x＞0），

由x=e时，f′（e）=0，且x＞e，e﹣x＞0，ex（1﹣lnx）＜0，

故f′（x）＜0，同理0＜x＜e，f′（x）＞0，

于是函数的单调增区间为（0，e），减区间为（e，+∞）．

解析

解析已在路上飞奔，马上就到！

知识点

利用导数证明不等式

题型：单选题

单选题 · 5 分

1.已知集合A={x|x2+3x+2≤0}，B={y|y=2x+1，x∈R}，则A∩RB=（）

A⌀

B{- 1}

C[- 2，- 1]

D[- 2，- 1)

正确答案

解析

∵A=[-2，-1]，B=(1，+∞)，

∴RB=(-∞，1]，即A∩RB=A.

知识点

利用导数证明不等式

题型：单选题

单选题 · 5 分

4.已知f(x)是定义在R上的可导函数，f'(x)为f(x)的导函数，又有两个向量m=(f(x),-1)，n=(1,f'(x)),且对于x∈R，两向量m,n的夹角范围都是[0, )，则（）

Ae2014f(-2014)<f(0),f(2015)>e2015f(0)

Be2014f(-2014)<f(0),f(2015)<e2015f(0)

Ce2014f(-2014)>f(0),f(2015)>e2015f(0)

De2014f(-2014)>f(0),f(2015)<e2015f(0)

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用导数证明不等式

题型：单选题

单选题 · 5 分

12.如图，在正方体ABCD-A1B1C1D1中B1E1=D1F1=，则 BE1与DF1所成角的余弦值是（）

正确答案

解析

过点A在平面ABB1A1内作AF,使得A1F=D1F1,则ADF1F是平行四边形，

∴FA∥DF1,再过点E1在平面ABB1A1内作E1E∥FA,则∠BE1E是BE1与DF1所成的角,∵BE1=D1F1=,ABCD-A1B1C1D1是正方体,∴E1B=又DF1=AF=E1E,DF1=BE1,

在△BE1E中,cos∠BE1E=

知识点

利用导数证明不等式

题型：简答题

简答题 · 12 分

17．已知函数的最小正周期为π，且当x=时，函数有最小值．

（1）求f（x）的解析式；

（2）作出f（x）在[0，π]范围内的大致图象．

正确答案

（1）f（x）=1–sin

（2）略

解析

解析已在路上飞奔，马上就到！

知识点

利用导数证明不等式

题型：简答题

简答题 · 12 分

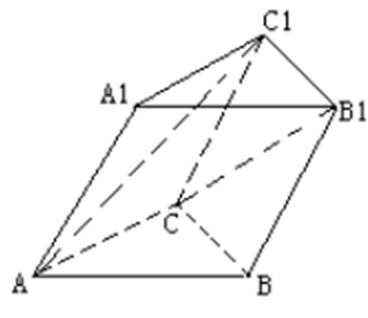
19．如图所示，已知斜三棱柱ABC-A1B1C1的各棱长均为2，侧棱与底面所成角为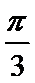，且侧面ABB1A1垂直于底面．

（1）判断B1C与C1A是否垂直，并证明你的结论；

（2）求四棱锥B-ACC1A1的体积。

正确答案

（1）几种常见处理方法：用空间直角坐标系解、传统方法解、基向量解．

（2）

解析

解析已在路上飞奔，马上就到！

知识点

利用导数证明不等式

继续学习学习下一知识点

下一知识点 : 利用导数求参数的取值范围

百度题库 > 高考 > 文科数学 > 利用导数证明不等式

扫码查看完整答案与解析