利用导数证明不等式_章节学习

1

题型：简答题

|

简答题 · 14 分

21．

设函数f(x)=ax2－a－lnx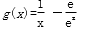，，其中a∈R，e=2.718…为自然对数的底数。

（Ⅰ）讨论f(x)的单调性；

（Ⅱ）证明：当x＞1时，g(x)＞0；

（Ⅲ）确定a的所有可能取值，使得f(x)＞g(x)在区间（1，+∞）内恒成立。

正确答案

知识点

利用导数研究函数的单调性利用导数求函数的极值利用导数求函数的最值利用导数证明不等式

1

题型：简答题

|

简答题 · 12 分

20. 已知函数.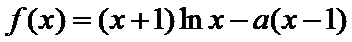

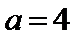
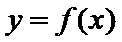
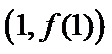
（I）当时，求曲线在处的切线方程；

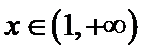
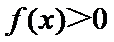
(II)若当时，，求的取值范围.

正确答案

知识点

导数的几何意义利用导数研究函数的单调性利用导数证明不等式

1

题型：简答题

|

简答题 · 18 分

22．若给定椭圆C：ax2+by2=1（a>0，b>0，ab）和点N（x0，y0），则称直线l：ax0x+by0y=1为椭圆C的“伴随直线”，

（1）若N（x0，y0）在椭圆C上，判断椭圆C与它的“伴随直线”的位置关系（当直线与椭圆的交点个数为0个、1个、2个时，分别称直线与椭圆相离、相切、相交），并说明理由；

（2）命题：“若点N（x0，y0）在椭圆C的外部，则直线l与椭圆C必相交．”写出这个命题的逆命题，判断此逆命题的真假，说明理由；

（3）若N（x0，y0）在椭圆C的内部，过N点任意作一条直线，交椭圆C于A、B，交l于M点（异于A、B），设，，问是否为定值？说明理由。

正确答案

（1）

即ax2–2ax0x+ax02=0

∴△=4a2x02–4a2x02=0

∴l与椭圆C相切．

（2）逆命题：若直线l：ax0x+by0y=1与椭圆C相交，则点N（x0，y0）在椭圆C的外部，是真命题。

联立方程得（aby02+a2x02）x2–2ax0x+1–by02=0

则△=4a2x02–4a（by02+ax02）（1–by02）>0

∴ax02–by02+b2y04–ax02+abx02y02>0

∴by02+ax02>1

∴N（x0，y0）在椭圆C的外部．

（3）同理可得此时l与椭圆相离，

设M（x1，y1），A（x，y）

则

代入椭圆C：ax2+by2=1，

利用M在l上，

即ax0x1+by0y1=1，

整理得（ax02+by02–1）12+ax12+by12–1=0

同理得关于2的方程，类似．

即1、2是（ax02+by02–1）2+ax12+by12–1=0的两根

∴1+2=0．

解析

解析已在路上飞奔，马上就到！

知识点

利用导数证明不等式

1

题型：简答题

|

简答题 · 12 分

21.已知函数f(x)= -ln x(a0). （1）求函数f(x)的单调区间；（2）当a = l时，求f(x)在区间[,2]上的最大值和最小值(0.69<ln 2<0.70)；（3）求证ln ≤

正确答案

1）函数的定义域为，

若，

故，函数在区间上单调递减，

时，在区间上单调递增，在上单调递减所以单调递减区间为

（2）时，，

由（1）可知，在上单调递增，在区间[1,2]上单调递减，

所以在区间上的最大值为而

故函数在区间上的最小值为

（3）由（2）可知，函数在区间（0,1）上单调递增，

故有

解析

f(x)求导并整理，得到f(x)在x>0区间上单调递减，然后分类讨论a的不同取值对单调区间的影响。利用函数单调性证明不等式恒成立的条件。

考查方向

本题主要考查函数的单调性和函数的最值。

解题思路

本利用导数求单调区间，利用函数与不等式关系求最大值最小值

易错点

不会利用导数求函数单调区间。

知识点

利用导数研究函数的单调性利用导数求函数的最值利用导数证明不等式

1

题型：简答题

|

简答题 · 12 分

21.设函数在点处的切线方程为．（自然对数的底数

（Ⅰ）求值，并求的单调区间；

（Ⅱ）证明：当时，．

正确答案

（Ⅰ），在单调递减，在单调递增

（Ⅱ）略

解析

（Ⅰ），

由已知，，，故，，

，当时，，当时，，

故在单调递减，在单调递增；……（6分）

（Ⅱ）方法1：不等式，即，

设，，

时，，时，，

所以在递增，在递减，

当时，有最大值，

因此当时，．

方法2：设，

在单调递减，在单调递增，

因为，，，

所以在只有一个零点，且，，

当时，，当时，，

在单调递减，在单调递增，

当时，，

因此当时，．

考查方向

本题主要考查函数的导数与切线间的关系，利用导数判断函数的单调性，以及构造函数解决不等式问题，难度较大，属高考重要考点。函数与导数的问题常常考察切线问题、函数的单调性、求参数的取值范围以及构造函数解决函数不等式问题。

解题思路

第一问直接求导得到在x=0时斜率为-1得到一个方程，函数图像过点（0，-1）得到第二个方程，解出a,b;

第二问直接变形后作商得到，然后对左边函数进行求导即得

易错点

在第二问采用作差来比较大小，求导后得到的函数无法求出零点，不能联系第一问求二阶导数，导致无法计算。

知识点

导数的几何意义利用导数研究函数的单调性利用导数证明不等式

1

题型：简答题

|

简答题 · 12 分

21.已知函数f(x)= -ln x(a0).

（1）求函数f(x)的单调区间；

（2）当a = l时，求f(x)在区间[,2]上的最大值和最小值(0.69<ln 2<0.70)；

（3）求证ln ≤

正确答案

（1）函数的定义域为，

若，又

故，函数在区间上单调递减，

时，在区间上单调递增，

在上单调递减所以单调递减区间为

（2）时，，

由（1）可知，在上单调递增，

在区间[1,2上单调递减，

所以在区间上的最大值为

而

故函数在区间上的最小值为

（3）由（2）可知，

函数在区间（0,1）上单调递增，

故有，

解析

将f(x)求导并整理，

得到f(x)在x>0区间上单调递减，

然后分类讨论a的不同取值对单调区间的影响。

利用函数单调性证明不等式恒成立的条件。

解题步骤见答案。

考查方向

本题主要考查函数的单调性和函数的最值。

解题思路

本利用导数求单调区间，利用函数与不等式关系求最大值最小值

易错点

不会利用导数求函数单调区间。

知识点

利用导数研究函数的单调性利用导数求函数的最值利用导数证明不等式

1

题型：简答题

|

简答题 · 12 分

21．已知函数（其中，是自然对数的底数），为导函数．

（Ⅰ）当时，求曲线在点处的切线方程；

（Ⅱ）若，试证明：对任意，恒成立．

正确答案

见解析

解析

本题属于导数应用中的基本问题，题目的难度是逐渐由易到难，（1）直接按照步骤来求；（2）要注意对参数的讨论．

（Ⅰ）由得，，所以曲线在点处的切线斜率为，，

曲线切线方程为，即．

（Ⅱ）由，得，令，所以，，因此，对任意，等价于，

由，，得，，

因此，当时，，单调递增；时，，单调递减，

所以的最大值为，故，

设，，所以时，，单调递增，，故时，，即，

所以．

因此，对任意，恒成立．

考查方向

本题考查了利用导数的几何意义和综合应用，分类讨论，讨论点大体可以分成以下几类：

（1）根据判别式讨论；

（2）根据二次函数的根的大小；

（3）定义域由限制时，根据定义域的隐含条件；

（4）求导形式复杂时取部分特别常常只需要转化为一个二次函数来讨论；

（5）多次求导求解等．

解题思路

本题考查导数的几何意义和综合应用，解题步骤如下：

（1）求导，然后求切线方程。

（2）对参数分类讨论证得结论。

易错点

第二问中的易丢对x的分类讨论。

知识点

导数的几何意义利用导数证明不等式

1

题型：简答题

|

简答题 · 14 分

21．己知函数f(x)=a（x-）-2lnx，其中a∈R．

(1)若f(x)有极值，求a的取值范围；

(2)若f(x)有三个不同的零点x1,x2,x3，求证：

(参考数值：ln2≈0. 6931)

正确答案

（1）0<a<1；（2）当a≤0或a≥1时，有唯一零点；当0<a<1时，有三个零点．

解析

试题分析：本题属于导数应用中的基本问题，题目的难度是逐渐由易到难，（1）直接按照步骤来求；（2）要注意对参数的讨论．

（1），因为f(x)定义域为（0，+∞），

所以ax2-2x+a=0有正根且不为等根。显然a≠0,由x1x2=1>0.得Δ>0且x1+x2>0,

所以 0<a<1 。

考查方向

本题考查了利用导数求含参数的函数极值，分类讨论，讨论点大体可以分成以下几类：（1）根据判别式讨论；（2）根据二次函数的根的大小；3、定义域由限制时，根据定义域的隐含条件；4、求导形式复杂时取部分特别常常只需要转化为一个二次函数来讨论；5、多次求导求解等．

解题思路

本题考查导数的性质，解题步骤如下：

（1）求导，然后解导数不等式，算极值。

（2）对参数分类讨论求得零点个数。

易错点

第二问中的易丢对a的分类讨论。

知识点

利用导数求函数的极值利用导数证明不等式利用导数求参数的取值范围

1

题型：简答题

|

简答题 · 16 分

20．已知为实常数，函数.

（1）讨论函数的单调性；

（2）若函数有两个不同的零点；

①求实数的取值范围；

②求证：.

正确答案

见解析

解析

（1）的定义域为．其导数．

①当时，，函数在上是增函数；

②当时，在区间上，；在区间上，．

所以在是增函数，在是减函数.

（2）①由（I）知，当时，函数在上是增函数，不可能有两个零点;

当时，在是增函数，在是减函数，此时为函数的最大值，当时，最多有一个零点，

所以，解得，

此时，，且，

令，则，

所以在上单调递增，所以，即

所以的取值范围是

②证法一：

下面证明：当时， .

设，则 .

在上是增函数，所以当时， .

即当时，..

.

②证法二：

令

则：，

所以函数在区间上为减函数.

,则,又

于是.

又由(1)可知 .即

考查方向

本题主要考查了导数的应用——利用导数求函数单调性，根据函数的零点求参数的取值范围。

解题思路

1利用导数求函数单调性，2根据函数的零点求参数的取值范围

3构造函数求两个零点和的范围

易错点

本题必须注意函数的定义域，以及对参数进行讨论，否则求解错误。

知识点

利用导数研究函数的单调性利用导数求函数的极值利用导数证明不等式

1

题型：简答题

|

简答题 · 12 分

21. 设函数，（）

（Ⅰ）当时，求函数的单调区间；

（Ⅱ）当，时，求证：

正确答案

函数单调减区间为：（Ⅰ），（Ⅱ）略

解析

试题分析：本题属于导数应用中的基本问题，题目的难度是逐渐由易到难，（1）直接按照步骤来求（2）涉及恒成立问题，转化成求函数的最值，这种思路是一般解法，往往要利用“分离参数法”；（3）零点回代是对学生是一种较高的要求．

（Ⅰ）函数的定义域为，

当时，，令：，

得：或，

所以函数单调增区间为：，

，得：，

所以函数单调减区间为：，

（Ⅱ）若证，成立，只需证：

即：当时成立

设∴，

显然在内是增函数且，∴=0在（1,2）内有唯一零点，

使得：，且当（1，），<0；当（，+），>0.∴在（1，）递减，在（，+）递增==

∵∴ ∴

∴成立

考查方向

本题考查了利用导数求函数单调区间的知识，第二问是证明题，过程中要对不等式进行等价变形，本题难在求导后零点不好求，要由零点定理对导数的零点进行分析，将零点关系式回代原函数，求出原函数的正负。

解题思路

1、求导，然后解导数不等式，算极值。

2、对不等式进行等价变形，转化为一个常见函数再进行求导；

3、零点回代。

易错点

1、第二问中卡在求导后解不出零点。2、设出零点后得出零点关系式代入原函数后的正负难以判断。

知识点

利用导数研究函数的单调性利用导数证明不等式

热门试卷

正确答案

知识点

正确答案

知识点

正确答案

解析

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点