- 利用导数证明不等式
- 共265题
已知函数
(1)当a=1时,∃x0∈[1,e]使不等式f(x0)≤m,求实数m的取值范围;
(2)若在区间(1,+∞)上,函数f(x)的图象恒在直线y=2ax的下方,求实数a的取值范围。
正确答案
见解析。
解析
(1)当a=1时,
可知当x∈[1,e]时f(x)为增函数,
最小值为
要使∃x0∈[1,e]使不等式f(x0)≤m,即f(x)的最小值小于等于m,
故实数m的取值范围是
(2)已知函数
若在区间(1,+∞)上,函数f(x)的图象恒在直线y=2ax的下方,
等价于对任意x∈(1,+∞),f(x)<2ax,
即
设
即g(x)的最大值小于0.
(1)当

∴
∴g(1)=﹣a﹣
∴a≥﹣
∴
(2)a≥1时,

g(x)无最大值,即最大值可无穷大,故此时不满足条件。
(3)当


同样最大值可无穷大,不满足题意,综上,实数a的取值范围是
知识点
某中学高三从甲.乙两个班中各选出7名学生参加数学竞赛,他们取得的成绩(满分l00分)的茎叶图如图,其中甲班学生成绩的众数是85,乙班学生成绩的中位数是83,则x+y的值为
正确答案
解析
略
知识点
为确保信息安全,信息需加密传输,发送方由明文



正确答案
解析
由已知,得:

知识点
电视传媒公司为了解某地区观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名.下面是根据调查结果绘制的观众日均收看该体育节目时的间频率分布表(时间单位为:分):
将日将收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.
(1)根据已知条件完成下面的2×2列联表,并据此资料你是否认为“体育迷”与性别有关?
(2)将日均收看该体育节目不低于50分钟的观众称为“超级体育迷”,已知“超级体育迷”中有2名女性,若从“超级体育迷”中任意选取2人,求至少有1名女性观众的概率.
正确答案
见解析。
解析
知识点
在同一平面直角坐标系中,已知函数




正确答案
解析
略
知识点
已知函数

(1)求函数





(2)讨论函数
正确答案
见解析。
解析
(1)




作




所以






(2)









若



若




若





当






综上所述,当






知识点
设函数
(1)已知曲线




(2)讨论函数
(3)在(1)的条件下,求证:对于定义域内的任意一个

正确答案
见解析
解析
(1)


根据题意,
所以

解得
(2)
1)当



所以


2)当
若




若





综上所述,当







(3)由(1)可知
设


当






可见
所以



知识点
设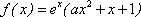
(1)若a>0,讨论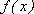
(2)x =1时,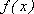
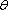
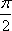
正确答案
见解析。
解析
知识点
某个年级有男生560人,女生420人,用分层抽样的方法从该年级全体学生中抽取一个容量为280的样本,则此样本中男生人数为 ▲ .
正确答案
160
解析
略
知识点
已知函数




(1)若函数


(2)证明:对任意的


正确答案
见解析。
解析
(1)若



当




令




由


综上知
(2)解法一 由(1)知函数


若

则

即


所以



解法二 构造函数


易知必有


又因为


故

即对任意的


知识点
扫码查看完整答案与解析