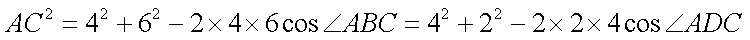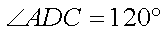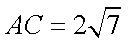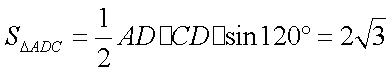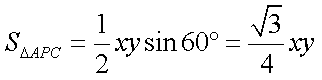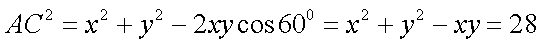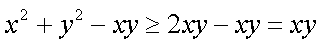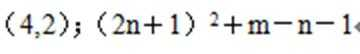- 利用导数证明不等式
- 共265题
已知

(1)求
(2)若


正确答案
见解析
解析
解析:(1)设


由
得
解得

∴

(2)当

当

∴
知识点
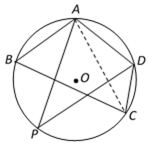
某市某棚户区改造建筑用地平面示意图如图所示,经规划调研确定,棚改规划建筑用地区域是半径为R的圆面,该圆面的内接四边形ABCD是原棚户

(1)请计算原棚户区建筑用地ABCD的面积及圆面的半径R的值;
(2)因地理条件的限制,边界AD、DC不能变更,而边界AB、BC可以调整,为了提高棚户区改造建筑用地的利用率,请在圆弧ABC上设计一点P,使得棚户区改造的新建筑用地APCD的面积最大,并求最大值。
正确答案
见解析
解析
(1) 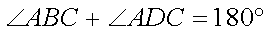
∴ 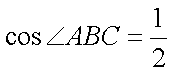
∵ 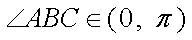
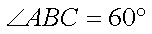
S四边形ABCD =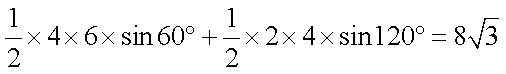
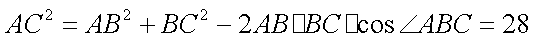
由正弦定理得: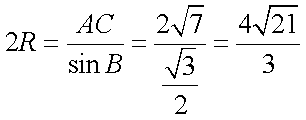
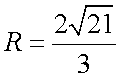
(2) S四边形APCD = 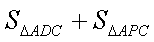
设AP = x,CP = y
由余弦定理得:
∴ 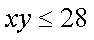
∴S四边
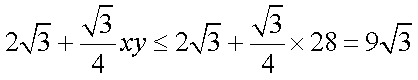
∴ 作AC的垂直平分线与圆弧ABC的交点即为点P,最大面积为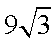
知识点
如图,将平面直角坐标系的格点(横、纵坐标均为整数的点)按如下规则标上数字标签:原点处标数字O,点(1,0)处标数字1,点(1,一1)处标数字2,点(O,-1)处标数字3,点(-1,-1)处标数字4,点(-1,0)处标数字5,点(-1,1)处标数字6,点
(0,1)处标数字7,…以此类推,①标数字50的格点的坐标为____。
②记格点坐标为(m,咒)的点(m、n均为正整数)处所标的数字为f(m,n),若n>m,则f(m,n)= ____。
正确答案
解析
f(1,0)=12,f(2,1)=32,f(3,2)=52,…,f(n+1,n)=(2n+1)2。
∵n>m,∴n≥m-1,∴当n>m时,f(m,n)=(2n+1)2+m-n-1。
知识点
已知函数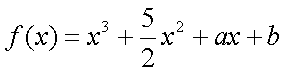
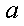
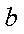
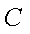
(1)当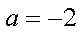
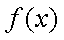
(2)设函数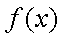
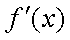
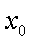
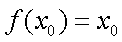
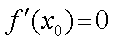
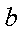
(3)已知点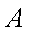
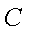
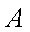
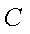
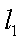
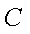
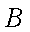
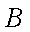
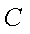
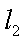
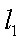
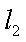
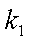
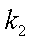
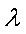
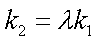
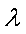
正确答案
见解析。
解析
(1)当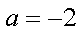
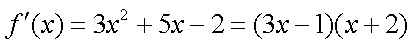
令f (x)<0,解得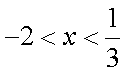
f(x)的单调减区间为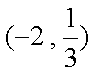
(2) 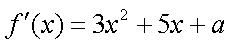
由题意知
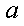
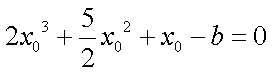
令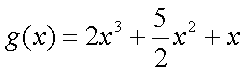
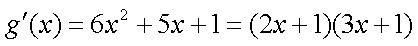
解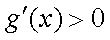

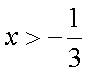
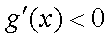
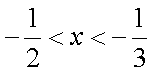
所以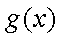

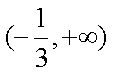
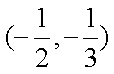
又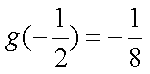
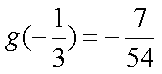
故实数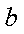
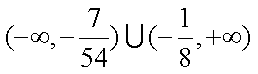
(3)设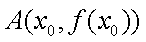
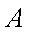
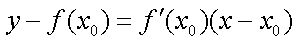
与曲线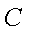
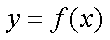
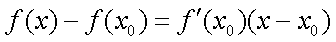
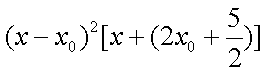
所以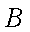
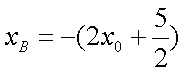
由题意知,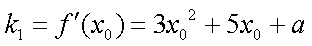
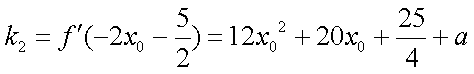
若存在常数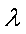
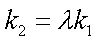
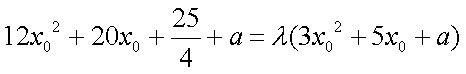
即存在常数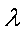
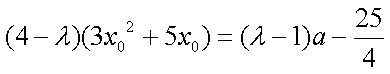
所以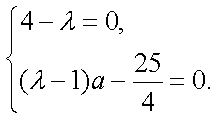
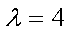

故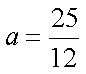
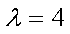
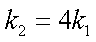
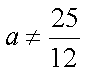
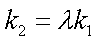
知识点
已知数列


(1)求数列

(2)若对每一个正整数


①求

②记






正确答案
见解析
解析
解:(1)因为





又当n=1时,

(2)①由(1)得
(i)若



此时
(ii)若


(iii)若




此时
综上所述,


②(i)当



当


(ii)当










所以此时满足题意的最大正整数
知识点
已知
正确答案
解析
∵








知识点
若圆锥底面半径为1,高为2,则圆锥的侧面积为 。
正确答案

解析
∵圆锥的底面半径为1,高为2,
∴母线长为:
∴圆锥的侧面积为:πrl=π×1×

知识点
下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程


③线性回归方程

④在一个
本题可以参考独立性检验临界值表
正确答案
解析
①③④正确,②回归方程


知识点
设函数
(1)当a=l时,求函数
(2)当a

(3)若对任意a∈(2,3)及任意

实数m的取值范围。
正确答案
见解析
解析
解析:(1)函数的定义域为
当

当





(2)

当


当


令
当

综上,当

当


(3)由(2)知,当

当




而

知识点
函数



正确答案
解析
由图象可知









知识点
扫码查看完整答案与解析