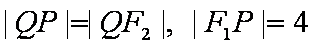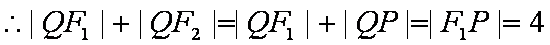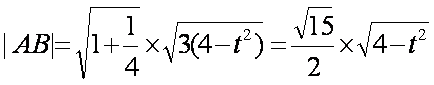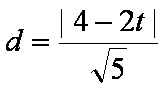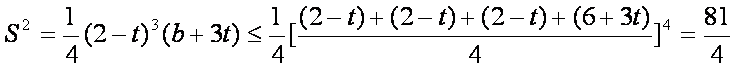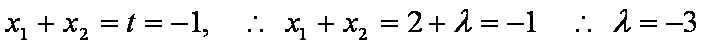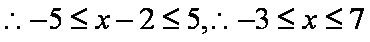- 利用导数证明不等式
- 共265题
已知向量


(1)求

(2)在△ABC中,角A,B,C的对边分别为a,b,c, 



正确答案
见解析。
解析
(1)

由


因为




(2)由


因为

因为

根据余弦定理

所以

知识点
已知P是圆F1: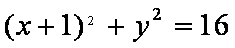

(1)当点P在圆上运动时,求点Q的轨迹C的方程。
(2)已知点M(1,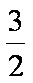
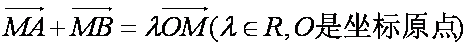
(i)求直线AB的斜率;
(ii)求证:当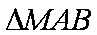
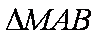
正确答案
见解析
解析
解析:(1)根据题设有
又
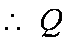
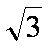
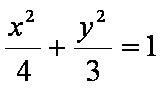
(2)(i)设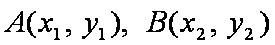
由 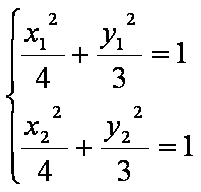
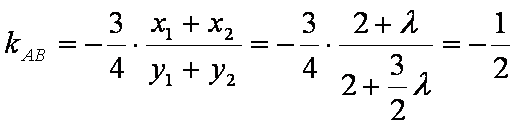
(ii)设AB的直线方程为 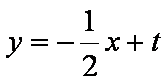
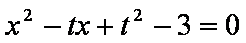
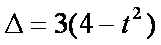
是P到直线AB的距离

求最值方法一:
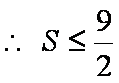

求最值方法二:导数法 此处略。
根据韦达定理得
故O是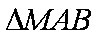
知识点
已知椭圆





(1)求椭圆
(2)过点








正确答案
见解析
解析
(1)正





依题意



∵ 
∴ 



(2)由(1)知,正


∴ 点
若直线









若直线







设

∴ 
∴ 




∵ 
∴ 


∴ 直线
综上,所求直线


知识点
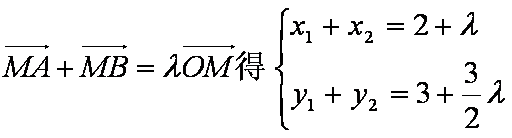
设点





(1)求椭圆
(2)设过右焦点






正确答案
(1)
解析
解析:
(1)解:设

所以 


则椭圆方程为 
又点
所以 

故椭圆方程为 
(2)解:由题意,直线

设直线

由 

得 
由题意,可知


所以直线



所以

即 
所以当



知识点
已知函数f(x)=
(1)当a=1时,求f(x)的单调区间;
(2)若对任意t∈[
正确答案
(1)
解析
(1)当a=1时,
由f′(x)>0得x<2,f′(x)<0得x>2
∴f(x)的单调递增区间为(﹣∞,2),单调递减区间为(2,+∞)。
(2)若对任意t∈[


即x∈[

设



设


∴h(x)在x∈[
即

∵
∴

∴

∴

∴a>
知识点
近年来玉制小挂件备受人们的青睐,某玉制品厂去年的年产量为10万件,每件小挂件的销售价格平均为100元,生产成本为80元,从今年起工厂投入100万元科技成本,并计划以后每年比上一年多投入100万元科技成本,预计产量每年递增1万件,设第



(1)求
(2)问从今年算起第几年的利润最高?最高利润为多少万元?
正确答案
见解析
解析
解析:(1)据题意,第




(2)令
当且仅当


故从今年起,第6年的利润最高,且最高利润为360(万元) (13分)
知识点
已知函数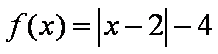
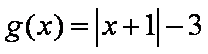
(1)若函数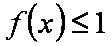
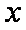
(2)若不等式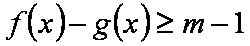
正确答案
见解析。
解析
(1)由题意得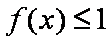


所以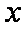
(2)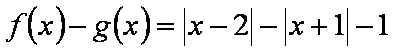
因为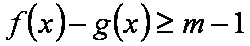
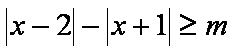
因为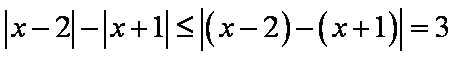
所以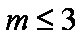
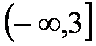
知识点
已知函数
(1)若

(2)设函数

(3)若在区间




正确答案
见解析。
解析
(1)当







所以单调减区间为

故

(2)

因为



若




若





所以此时单调减区间为

(Ⅲ)由第(2)问的解答可知只需在


若




若


若



令
即

设


当









知识点
已知关于








(1)列举出所有的数对

(2)求函数

正确答案
(1)
解析
解析:(1)

函数


所以函数

(2)函数





所以函数


知识点
如图甲,在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ACD=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC(如图乙),设点E、F分别为棱AC、AD的中点。
(1)求证:DC⊥平面ABC;
(2)设CD=a,求三棱锥A-BFE的体积。高中数学辅导网
正确答案
见解析
解析
解析:
(1)证明:在图甲中∵


即
在图乙中,∵平面ABD

∴AB⊥底面BDC,∴AB⊥CD。
又
∴DC
(2)解:∵E、F分别为AC、AD的中点
∴EF//CD,又由(Ⅰ)知,DC
∴EF⊥平面ABC,
∴
在图甲中,∵

由

∴
∴
知识点
扫码查看完整答案与解析