- 利用导数证明不等式
- 共265题
已知圆




正确答案
解析
试题分析:因为圆心在直线








知识点
已知函数
(1)当

(2)若对于任意


(3)若过点


正确答案
见解析
解析
(1)当


因为
所以当


当



所以函数



(2)方法1:由

因为对于任意

即对于任意

即对于任意

令


必须满足

即

所以实数

方法2:由

因为对于任意

所以问题转化为,对于任意

因为

①当



所以
由


②当




所以
由


综上①②可得,实数

(3)设点

则过点

所以过点

因为点
所以
即
若过点

则方程
令


令


因为

所以必须

所以实数

知识点
已知函数
(1)求不等式 
(2)若关于


正确答案
见解析。
解析
(1)原不等式等价于

解之得
即不等式的解集为
(2)


知识点
某校高三年级在5月份进行一次质量考试,考生成绩情况如下表所示:
已知用分层抽样方法在不低于550分的考生中随机抽取5名考生进行质量分析,其中文科考生抽取了2名。
( 1)求
(2)图6是文科不低于550分的6名学生的语文成绩的茎叶图,计算这6名考生的语文成绩的方差;
(3)已知该校不低于480分的文科理科考生人数之比为



正确答案
见解析
解析
解:(1)依题意

(2)
∴这6名考生的语文成绩的方差

(3)依题意

解得
知识点
集合


正确答案
解析
解不等式






知识点
已知函数
(1)求
(2)在△ABC中,角A、B、C的对边分别是a,b,c ,满足

正确答案
见解析。
解析
(1)由


由
故

(2)由






知识点
已知一个正四面体的俯视图如图所示,其中四边形

正确答案
解析
解析:这个正四面体的位置是AC放在桌面上,BD平行桌面,如图:
正四面体的棱长就是俯视图正方形的对角线的长,所以正四面体的棱长为6,
设正四面体的内切球的半径为


所以正四面体的内切球的表面积为 
故选:A
知识点
对任意的实数x,y,定义运算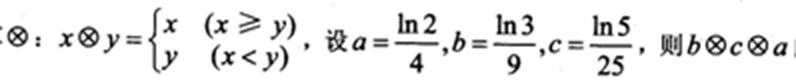
正确答案
解析
由运算
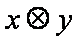
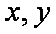
所以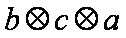
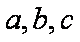
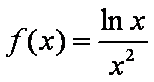

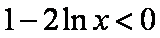
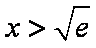
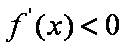
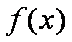
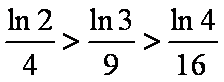
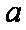
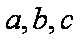
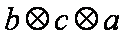
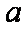
知识点
在直角坐标平面内,以坐标原点






(1)过极点作直线


(2)若点



正确答案
见解析
解析
(1)由直线的参数方程消去参数



设点


又


代入直线


所以点P的极坐标为
(2)因为曲线

所以曲线

则圆心



知识点
已知向量


正确答案
解析
试题分析:因为

②: 
由此得
知识点
扫码查看完整答案与解析
































