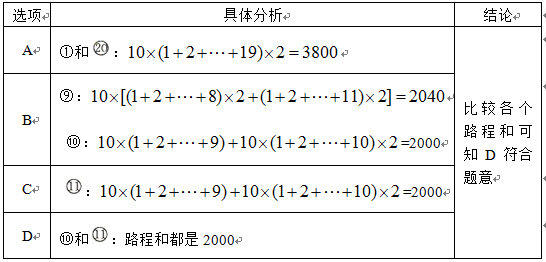- 与面积、体积有关的几何概型
- 共55题
A.若不等式
B.
正确答案
A.
解析
A.
当
当
当
综上可得
即实数
B.
知识点
根据以往统计资料，某地车主购买甲种保险的概率为0.5，购买乙种保险但不购买甲种保险的概率为0.3.设各车主购买保险相互独立。
（1）求该地1位车主至少购买甲、乙两种保险中的1种的概率；
（2）求该地的3位车主中恰有1位车主甲、乙两种保险都不购买的概率。
正确答案
见解析。
解析
（1）设事件A={购买甲种保险}，B={购买乙种保险}，C={至少购买甲、乙两种保险中的1种}。
因为
另解：
（2）
知识点
已知椭圆
（1）求椭圆的方程；
（2）若直线l：y=﹣
正确答案
（1）椭圆的方程为
（2）直线l的方程为
解析
（1）由题意可得
解得
∴椭圆的方程为
（2）由题意可得以F1F2为直径的圆的方程为x2+y2=1。
∴圆心到直线l的距离d=
由d＜1，可得
∴|CD|=2
设A（x1，y1），B（x2，y2）。
联立
化为x2﹣mx+m2﹣3=0，
可得x1+x2=m，
∴|AB|=
由
解得
因此直线l的方程为
知识点
植树节某班20名同学在一段直线公路一侧植树，每人植一棵，相邻两棵树相距10米，开始时需将树苗集中放置在某一树坑旁边，现将树坑从1到20依次编号，为使各位同学从各自树坑前来领取树苗所走的路程总和最小，树苗可以放置的两个最佳坑位的编号为（ ）
A①和
B⑨和⑩
C⑨和
D⑩和
正确答案
解析
（方法一）
（方法二）根据图形的对称性，树苗放在两端的树坑旁边，所得路程总和相同，取得一个最值；所以从两端的树坑向中间移动时，所得路程总和的变化相同，最后移到第10个和第11个树坑旁时，所得的路程总和达到另一个最值，所以计算两个路程和进行比较即可。树苗放在第一个树坑旁，则有路程总和是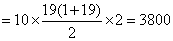
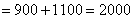
知识点
如图，矩形ABCD中，点E为边CD的重点，若在矩形ABCD内部随
机取一个点Q，则点Q取自△ABE内部的概率等于
A
B
C
D
正确答案
解析
知识点
扫码查看完整答案与解析