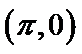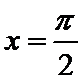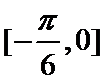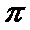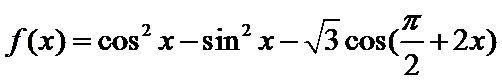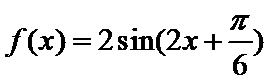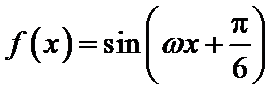- 三角函数的周期性及其求法
- 共131题
6．已知函数f（x）=cosxsinx（x∈R），给出下列四个命题（ ）
①若f（x1）=﹣f（x2），则x1=﹣x2；
②f（x）的最小正周期是2π；
③f（x）在区间[﹣
④f（x）的图象关于直线x=
正确答案
解析
解：∵f（x）=cosxsinx=
若f（x1）=﹣f（x2），则sin2x1=﹣sin2x2=sin（﹣2x2）
∴2x1=﹣2x2+2kπ时满足条件，即x1+x2=kπ可以，故①不正确；
T=
令
当k=0时，x∈[﹣
将x=
故f（x）的图象关于直线x=
故选D．
知识点
15．已知
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3.函数
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
15．已知a＝（sinx，－cosx），b＝（cosx，
（1）求f（x）的最小正周期，并求其图像对称中心的坐标；
（2）当0≤x≤
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
17.已知函数
（Ⅰ）求函数
（Ⅱ）设
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
17．已知函数
（1）求函数
（2）求函数
（3）求函数
正确答案
解：
（1）
（2）
（3）令
则
所以函数
解析
解析已在路上飞奔，马上就到！
知识点
11.
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
23．对于定义域为
（1）验证
（2）设
（3）证明：“
正确答案
（1）详见解析
（2）详见解析
（3）详见解析
解析
（2）由于
若
（3）若
同理，若
以下证明最后一部分结论.
由（2）所证知存在
而
类似地，当
结论成立.
知识点
7．定义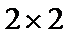
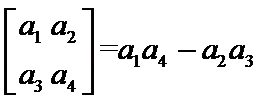
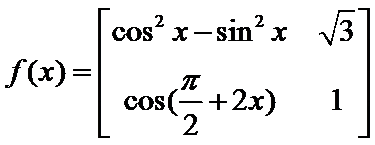
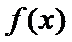
A图象关于
B图象关于直线
C在区间
D周期为
正确答案
解析
根据矩阵的定义，可以得到
所以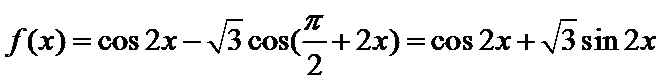
根据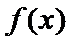
考查方向
三角函数
解题思路
先根据矩阵的定义，得到f(x)的解析式，然后根据函数的解析式判断函数的相关性质.
易错点
三角函数公式记忆混淆
知识点
4.如果函数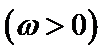
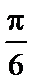
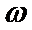
正确答案
解析
因为三角函数两相邻零点间的距离为半个周期，所以由相邻两个零点之间的距离为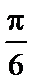
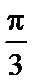
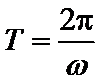
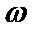
考查方向
解题思路
相邻两个零点之间的距离为半个周期，因此就可求出周期来，结合
易错点
本题易在处理两相邻零点间的距离时出错，不能将其与函数周期结合 。
知识点
扫码查看完整答案与解析