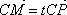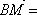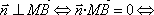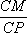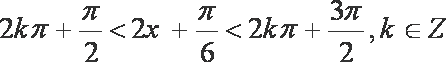- 正弦函数的图象
- 共33题
△ABC中,角A、B、C的对边分别为


正确答案
-1
解析
略
知识点
把函数


正确答案
解析



再将图象向右平移


故选A。
知识点
已知点M是⊿ABC的重心,若A=60°,

正确答案
解析
∵




知识点
如图,圆





若


正确答案
解析
略
知识点
对于函数f(x)=2sinxcosx,下列选项中正确的是 【】
正确答案
解析
本题考查三角函数的性质
f (x)=2sinxcosx=sin2x,周期为π的奇函数
知识点
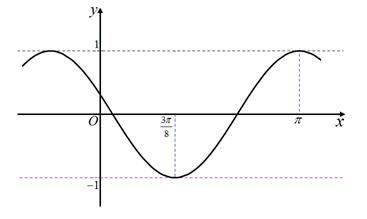
如图,阴影区域是由函数
正确答案
解析
略
知识点
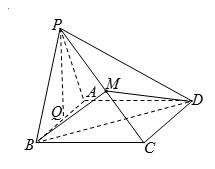
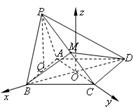
如图,四棱锥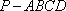

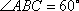
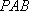
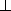
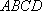
(1)设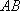
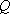
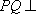
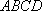
(2)求斜线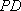
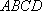
(3)在侧棱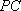
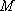
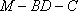
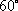
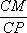
正确答案
见解析
解析
(1)证明:因为侧面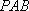
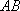
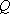
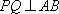
因为侧面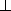
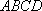

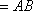
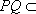
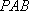
所以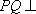
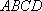
(2)连结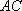
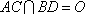
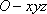
则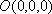
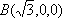
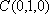
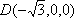
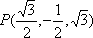
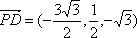
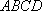
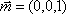
设斜线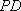
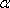
则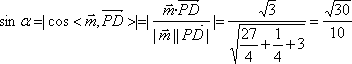
(3)设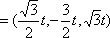
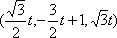
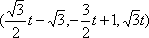
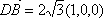
设平面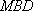
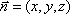
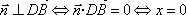
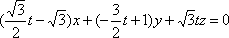
取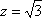
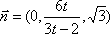
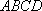
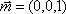
所以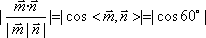
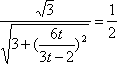
解得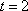
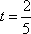
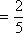
知识点
已知函数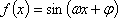
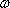
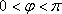
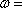
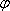
正确答案

解析
略
知识点
在△ABC中,a,b,c是角A,B,C对应的边,向量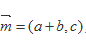
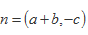
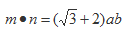
(1)求角C;
(2)函数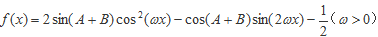
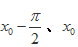
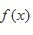
正确答案
见解析
解析
解析:(1)因为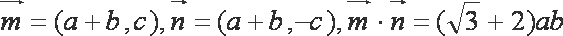
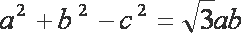
故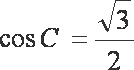
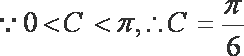
(2)
=
=
=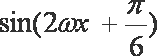
因为相邻两个极值的横坐标分别为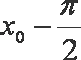
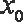
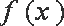
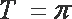
所以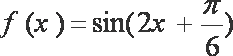
由
所以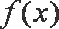
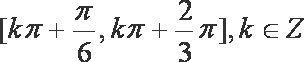
知识点
已知△ABC的三内角A、B、C所对的边的长分别为a、b、c,设向量
(1)求
(2)若
正确答案
(1)
解析
(1)∵
∴
由余弦定理得:
又∵

(2)∵
∴

∴a<b ∴A<B
∴


∴

知识点
扫码查看完整答案与解析